题目内容
10. 如图所示,在竖直向下的匀强电场中有一绝缘的光滑离心轨道,一个带负电的小球从斜轨道上的A点由静止释放,沿轨道滑下,已知小球的质量为m,电量为-q,匀强电场的场强大小为E,斜轨道的倾角为α(小球的重力大于所受的电场力).
如图所示,在竖直向下的匀强电场中有一绝缘的光滑离心轨道,一个带负电的小球从斜轨道上的A点由静止释放,沿轨道滑下,已知小球的质量为m,电量为-q,匀强电场的场强大小为E,斜轨道的倾角为α(小球的重力大于所受的电场力).(1)求小球沿斜轨道下滑的加速度的大小.
(2)若使小球通过圆轨道顶端的B点,求A点距水平地面的高度h至少应为多大?
(3)若小球从斜轨道h=5R处由静止释放.假设其能够通过B点,求在此过程中小球机械能的改变量.
分析 (1)对小球进行受力分析,由牛顿第二定律即可求出加速度;
(2)小球恰好通过最高点,则由向心力公式可求得B点的速度;对AB过程由动能定理可得A在轨道上的高度;
(3)小球由h=5R处到B过程中小球机械能的改变量等于电场力做的功.
解答 解:(1)根据牛顿第二定律:
(mg-qE)sinα=ma,解得:a=$\frac{(mg-qE)sinα}{m}$;
(2)若小球刚好通过B点不下落,据牛顿第二定律有:mg-qE=m$\frac{{v}^{2}}{R}$ ①
小球由A到B,据动能定理:(mg-qE)(h-2R)=$\frac{1}{2}$mv2-0 ②
①②式联立,得h=2.5R;
(3)小球从静止开始沿轨道运动到B点的过程中,由功能关系知,
机械能的变化量为:△E机=W电,W电=-3EqR,故△E机=-3EqR
答:(1)求小球沿斜轨道下滑的加速度的大小为$\frac{(mg-qE)sinα}{m}$;
(2)若使小球通过圆轨道顶端的B点时不落下来,求A点距水平地面的高度h至少应为2.5R;
(3)若小球从斜轨道h=5R 处由静止释放.假设其能够通过B点,求在此过程中小球机械能的改变量-3EqR.
点评 本题考查动能定理及向心力公式的应用,在解题时注意计算中的中间过程不必解出,而应联立可以简单求出.

练习册系列答案
相关题目
2.下列说法正确的是( )
| A. | 地面附近有一高速水平飞过的火箭,地面上的人观察到的“火箭长度”要比火箭上的人观察到的“火箭长度”短一些 | |
| B. | 拍摄玻璃橱窗内的物品时,往往在镜头前加一个偏振片以增加透射光的强度 | |
| C. | 变化的电场-定产生变化的磁场,变化的磁场一定产生变化的电场 | |
| D. | 单摆在周期性外力作用下做受迫振动,其振动周期与单摆的摆长有关 | |
| E. | 次声波是频率低于20Hz的声波,它比超声波更易发生衍射 | |
| F. | 一列加速驶出车站的火车,站台上的人听到的汽笛音调变高了 |
15. 在10月24日,南京选手王冬强在第七届城市运动会上以13秒38的成绩获得男子110米栏冠军,刘翔师弟陆嘉腾13秒41获得第二.如图所示是两名选手在比赛中的情景.下列说法正确的是( )
在10月24日,南京选手王冬强在第七届城市运动会上以13秒38的成绩获得男子110米栏冠军,刘翔师弟陆嘉腾13秒41获得第二.如图所示是两名选手在比赛中的情景.下列说法正确的是( )
 在10月24日,南京选手王冬强在第七届城市运动会上以13秒38的成绩获得男子110米栏冠军,刘翔师弟陆嘉腾13秒41获得第二.如图所示是两名选手在比赛中的情景.下列说法正确的是( )
在10月24日,南京选手王冬强在第七届城市运动会上以13秒38的成绩获得男子110米栏冠军,刘翔师弟陆嘉腾13秒41获得第二.如图所示是两名选手在比赛中的情景.下列说法正确的是( )| A. | 在110 m栏比赛中,选手通过的路程就是位移 | |
| B. | 王冬强在起跑过程中的加速度一定比陆嘉腾的大 | |
| C. | 王冬强在全程中的平均速度约为8.22 m/s | |
| D. | 冲到终点时,王冬强的速度一定大于陆嘉腾的速度 |
2.从发现情况到采取相应措施经过的时间叫人的反应时间.现甲同学用两根手指捏住木尺顶端,乙同学一只手在木尺下端靠近木尺但不接触木尺且准备握住木尺.当乙同学看到甲同学放手时,立即握住木尺,测出木尺下落高度为19.6cm,g=9.8m/s2,则( )
| A. | 甲同学反应时间为0.2s | B. | 甲同学反应时间为2s | ||
| C. | 乙同学反应时间为0.2s | D. | 乙同学反应时间为2s |
19. 如图所示,a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知a点电势为20V,b点电势为24V,d点电势为12V,一个质子(${\;}_{1}^{1}$H)从b点以 v0的速度射入此电场,入射方向与bc成45°角,一段时间后经过c点.不计质子的重力,下列判断正确的是( )
如图所示,a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知a点电势为20V,b点电势为24V,d点电势为12V,一个质子(${\;}_{1}^{1}$H)从b点以 v0的速度射入此电场,入射方向与bc成45°角,一段时间后经过c点.不计质子的重力,下列判断正确的是( )
 如图所示,a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知a点电势为20V,b点电势为24V,d点电势为12V,一个质子(${\;}_{1}^{1}$H)从b点以 v0的速度射入此电场,入射方向与bc成45°角,一段时间后经过c点.不计质子的重力,下列判断正确的是( )
如图所示,a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知a点电势为20V,b点电势为24V,d点电势为12V,一个质子(${\;}_{1}^{1}$H)从b点以 v0的速度射入此电场,入射方向与bc成45°角,一段时间后经过c点.不计质子的重力,下列判断正确的是( )| A. | 电场强度的方向由d指向b | |
| B. | a点电势高于c点电势 | |
| C. | 质子从b运动到c,电场力做功为8eV | |
| D. | 质子从b运动到c,所用的时间为$\frac{{\sqrt{2}L}}{2v_0}$ |
20. 图示为高速摄影机拍摄到的子弹穿透苹果瞬间的照片.该照片经放大后分析出,在曝光时间内,子弹影像前后错开的距离约为子弹长度的1%~2%.已知子弹飞行速度约为1000m/s,由此可估算出这幅照片的曝光时间最接近( )
图示为高速摄影机拍摄到的子弹穿透苹果瞬间的照片.该照片经放大后分析出,在曝光时间内,子弹影像前后错开的距离约为子弹长度的1%~2%.已知子弹飞行速度约为1000m/s,由此可估算出这幅照片的曝光时间最接近( )
 图示为高速摄影机拍摄到的子弹穿透苹果瞬间的照片.该照片经放大后分析出,在曝光时间内,子弹影像前后错开的距离约为子弹长度的1%~2%.已知子弹飞行速度约为1000m/s,由此可估算出这幅照片的曝光时间最接近( )
图示为高速摄影机拍摄到的子弹穿透苹果瞬间的照片.该照片经放大后分析出,在曝光时间内,子弹影像前后错开的距离约为子弹长度的1%~2%.已知子弹飞行速度约为1000m/s,由此可估算出这幅照片的曝光时间最接近( )| A. | 10-3s | B. | 10-5s | C. | 10-7s | D. | 10-15s |
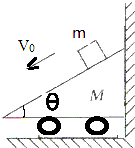 如图所示,质量为M的小车放在光滑的水平地面上,右面靠墙,上表面是一个光滑的斜面,斜面的倾角为θ,设当地的重力加速度为g,那么,当有一个质量为m的物块在这个斜面上以初速度为V0开始下滑后,求:
如图所示,质量为M的小车放在光滑的水平地面上,右面靠墙,上表面是一个光滑的斜面,斜面的倾角为θ,设当地的重力加速度为g,那么,当有一个质量为m的物块在这个斜面上以初速度为V0开始下滑后,求: