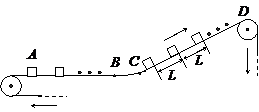题目内容
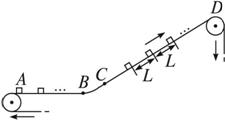
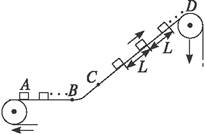
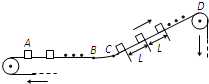 一传送带装置示意图如图,其中传送带AB段是水平的,CD段是倾斜的,动摩擦因数均为μ,AB段和CD段通过极短的BC段平滑连接.现将大量的质量均为m的小货箱一个一个在A处放到传送带上,放置时初速为零,经传送带运送到D处,D和A的高度差为h.稳定工作时传送带速度保持不变,始终为v,CD段上各箱等距排列,相邻两箱的距离为L.每个箱子在A处投放后,在到达B之前已经相对于传送带静止,且以后也不再滑动(忽略经BC段时的微小滑动).传送带由电动机带动,传送带与轮子间无相对滑动,不计轮轴处的摩擦.
一传送带装置示意图如图,其中传送带AB段是水平的,CD段是倾斜的,动摩擦因数均为μ,AB段和CD段通过极短的BC段平滑连接.现将大量的质量均为m的小货箱一个一个在A处放到传送带上,放置时初速为零,经传送带运送到D处,D和A的高度差为h.稳定工作时传送带速度保持不变,始终为v,CD段上各箱等距排列,相邻两箱的距离为L.每个箱子在A处投放后,在到达B之前已经相对于传送带静止,且以后也不再滑动(忽略经BC段时的微小滑动).传送带由电动机带动,传送带与轮子间无相对滑动,不计轮轴处的摩擦.(1)为了小货箱到达B点前相对于传动带静止,AB段至少多长?
(2)将每个小货箱从A点运送到D点,因摩擦产生了多少热量?
(3)求电动机的平均输出功率?
分析:(1)小货箱相对于传送带相对静止前,在滑动摩擦力作用下,做匀加速运动,由动能定理求解AB段最小长度.
(2)小货箱从释放到相对于传送带静止过程做匀加速运动,根据牛顿第二定律和运动学公式求出货箱与传送带的相对位移s相对大小,再根据sQ=fs相对求热量.
(3)根据相邻两箱的距离为L求出T时间内运送货箱的个数,再根据能量守恒定律求解电动机的平均输出功率.
(2)小货箱从释放到相对于传送带静止过程做匀加速运动,根据牛顿第二定律和运动学公式求出货箱与传送带的相对位移s相对大小,再根据sQ=fs相对求热量.
(3)根据相邻两箱的距离为L求出T时间内运送货箱的个数,再根据能量守恒定律求解电动机的平均输出功率.
解答:解:(1)小货箱相对于传送带相对静止前,由动能定理得:
μmgs=
mv2-0
解得:s=
;
(2)设小货箱从释放到相对于传送带静止需要时间t,则:
t=
=
这段时间传送带向右运动s′,s′=vt
所以货箱与传送带的相对位移s相对=s′-s
因摩擦产生的热量 Q=fs相对=
mv2;
(3)设T时间内运送货箱N个,则 N=
设每个货箱由A点运到D点需要能量E,E=Q+mgh
所以电动机的平均输出功率为 P=
=
=
(
mv2+mgh).
答:
(1)为了小货箱到达B点前相对于传动带静止,AB段至少长为
.
(2)将每个小货箱从A点运送到D点,因摩擦产生的热量为
mv2.
(3)电动机的平均输出功率是
(
mv2+mgh).
μmgs=
| 1 |
| 2 |
解得:s=
| v2 |
| 2gμ |
(2)设小货箱从释放到相对于传送带静止需要时间t,则:
t=
| v |
| a |
| v |
| gμ |
这段时间传送带向右运动s′,s′=vt
所以货箱与传送带的相对位移s相对=s′-s
因摩擦产生的热量 Q=fs相对=
| 1 |
| 2 |
(3)设T时间内运送货箱N个,则 N=
| vT |
| L |
设每个货箱由A点运到D点需要能量E,E=Q+mgh
所以电动机的平均输出功率为 P=
| NE |
| T |
N(
| ||
| T |
| v |
| L |
| 1 |
| 2 |
答:
(1)为了小货箱到达B点前相对于传动带静止,AB段至少长为
| v2 |
| 2gμ |
(2)将每个小货箱从A点运送到D点,因摩擦产生的热量为
| 1 |
| 2 |
(3)电动机的平均输出功率是
| v |
| L |
| 1 |
| 2 |
点评:题目看似很难,实际上是由一些简单的题目综合而成的,关键要正确分析物体的受力情况,运用力学基本规律,比如动能定理、牛顿第二定律和运动学公式等等求解.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
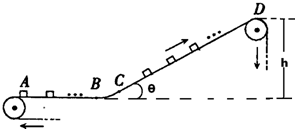 一传送带装置示意图如图,其中传送带经过AB区域时是水平的,经过BC区域时变为小圆弧形(圆弧由光滑模板形成,已画出),经过CD区域时是倾斜的倾角是θ,AB和CD都与BC相切.现将大量的质量均为m的小货箱一个一个在A处放到传送带上,放置时初速为零,经传送带运送到D处,D和A的高度差为h.稳定工作时传送带速度不变,CD段上各箱等距排列.每个箱子在A处投放后,在到达B之前已经相对于传送带静止,(忽略经BC段时的微小滑动),斜面与箱子的摩擦因数μ(小于tanθ),要使箱子能达到D端.已知在一段相当长的时间T内,共运送小货箱的数目为N.这装置由电动机带动,传送带与轮子间无相对滑动,不计轮轴处的摩擦.
一传送带装置示意图如图,其中传送带经过AB区域时是水平的,经过BC区域时变为小圆弧形(圆弧由光滑模板形成,已画出),经过CD区域时是倾斜的倾角是θ,AB和CD都与BC相切.现将大量的质量均为m的小货箱一个一个在A处放到传送带上,放置时初速为零,经传送带运送到D处,D和A的高度差为h.稳定工作时传送带速度不变,CD段上各箱等距排列.每个箱子在A处投放后,在到达B之前已经相对于传送带静止,(忽略经BC段时的微小滑动),斜面与箱子的摩擦因数μ(小于tanθ),要使箱子能达到D端.已知在一段相当长的时间T内,共运送小货箱的数目为N.这装置由电动机带动,传送带与轮子间无相对滑动,不计轮轴处的摩擦.