题目内容
1.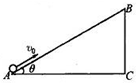 如图所示,长为L、倾角为θ的绝缘光滑斜面处于场强方向平行于纸面的电场中,一电荷量为q、质量为m的带负电小球,以初速度v0由斜面底端的A点开始沿斜面上滑,到达斜面顶端B点时速度为2v0.已知重力加速度为g,下列判断正确的是( )
如图所示,长为L、倾角为θ的绝缘光滑斜面处于场强方向平行于纸面的电场中,一电荷量为q、质量为m的带负电小球,以初速度v0由斜面底端的A点开始沿斜面上滑,到达斜面顶端B点时速度为2v0.已知重力加速度为g,下列判断正确的是( )| A. | 小球在B点的电势能大于小球在A点的电势能 | |
| B. | A、B两点的电势差UAB=$\frac{\frac{3}{2}m{{v}_{0}}^{2}+mgLsinθ}{q}$ | |
| C. | 该电场可能是位于AB中垂线上的电荷所形成的电场 | |
| D. | 若该电场是匀强电场,则电场强度最小值为$\frac{\frac{3}{2}m{{v}_{0}}^{2}+mgLsinθ}{qL}$ |
分析 根据动能定理和电场力做功公式结合,求解A、B两点的电势差.根据电场力做功的正负,判断小球电势能的大小,当电场力做正功时,小球电势能减小;相反,电势能增大.若电场是匀强电场,根据AB间的电势差确定电场强度的最小值,再确定场强的最小值.由电势关系,判断该电场是否由斜面中点正上方某点的点电荷Q产生的.
解答 解:A、小球从A运动到B,根据动能定理知,动能增加,重力做负功,则电场力做正功,可知电势能减小,小球在B点的电势能小于小球在A点的电势能,故A错误.
B、根据动能定理得:-mgLsinθ+qUAB=$\frac{1}{2}m(2{v}_{0})^{2}-\frac{1}{2}m{{v}_{0}}^{2}$,则${U}_{AB}=\frac{\frac{3}{2}m{{v}_{0}}^{2}+mgLsinθ}{q}$,故正确.
C、如果该电场是位于AB中垂线上的正电荷所形成的电场,则AB的电势相等,与A选项电势能减小矛盾,故C错误;
D、因为AB间的电势差${U}_{AB}=\frac{\frac{3}{2}m{{v}_{0}}^{2}+mgLsinθ}{q}$,该电场是匀强电场,当电场的方向平行斜面向上时,电场强度最小,E=$\frac{{U}_{AB}}{L}$=$\frac{\frac{3}{2}m{{v}_{0}}^{2}+mgLsinθ}{qL}$.故D正确.
故选:BD.
点评 解决本题的关键知道电场力做功与电势能的关系,结合动能定理进行求解,对于匀强电场,掌握电场强度的公式E=$\frac{U}{d}$,注意d为沿电场线方向的距离.

练习册系列答案
相关题目
12.摩托车通过质量不可忽略的钢丝绳拖动货物前行,下列说法中正确的是( )
| A. | 摩托车启动过程中,钢绳拉货物的力大于货物拉钢绳的力 | |
| B. | 摩托车启动过程中,摩托车拉钢绳的力大于钢绳拉货物的力 | |
| C. | 摩托车平稳(匀速)行驶过程中,摩托车拉钢绳的力等于钢绳拉货物的力 | |
| D. | 不论摩托车处于怎样的运动状态,摩托车拉钢绳的力与钢绳拉货物的力都相等 |
9.关于电场力做功,电势差和电势能,说法错误的是( )
| A. | 在电场中任意两点移动电荷时,电场力做功为零,那么这两点的电势差不一定为0 | |
| B. | 电荷只受电场力运动时,其电势能的减少,一定等于其动能的增加 | |
| C. | 电荷在电场力作用下移动过程中,电场力对电荷做正功,则电荷的电势能减小 | |
| D. | 电荷在电场力作用下移动过程中,电场力对电荷做负功,则电荷的电势能增加 |
6.下列有关黑体辐射和光电效应的说法中正确的是( )
| A. | 普朗克在研究黑体辐射问题时提出了能量子假说 | |
| B. | 在黑体辐射中,随着温度的升高,各种频率的辐射都增加,辐射强度极大值的光向频率较低的方向移动 | |
| C. | 用一束绿光照射某金属,能产生光电效应,现把这束绿光遮住一半,仍然可发生光电效应 | |
| D. | 在光电效应现象中,极限频率越大的金属材料逸出功越大 | |
| E. | 在光电效应现象中,入射光的强度越大,光电子的最大初动能越大 |
13.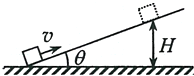 一物块沿倾角为θ的斜坡向上滑动.当物块的初速度为v时,上升的最大高度为H,如图所示;当物块的初速度为$\frac{v}{2}$时,上升的最大高度记为h.重力加速度大小为g.则物块与斜坡间的动摩擦因数μ和h分别为( )
一物块沿倾角为θ的斜坡向上滑动.当物块的初速度为v时,上升的最大高度为H,如图所示;当物块的初速度为$\frac{v}{2}$时,上升的最大高度记为h.重力加速度大小为g.则物块与斜坡间的动摩擦因数μ和h分别为( )
 一物块沿倾角为θ的斜坡向上滑动.当物块的初速度为v时,上升的最大高度为H,如图所示;当物块的初速度为$\frac{v}{2}$时,上升的最大高度记为h.重力加速度大小为g.则物块与斜坡间的动摩擦因数μ和h分别为( )
一物块沿倾角为θ的斜坡向上滑动.当物块的初速度为v时,上升的最大高度为H,如图所示;当物块的初速度为$\frac{v}{2}$时,上升的最大高度记为h.重力加速度大小为g.则物块与斜坡间的动摩擦因数μ和h分别为( )| A. | μ=tanθ | B. | μ=($\frac{{v}^{2}}{2gh}$-1)tanθ | C. | h=$\frac{H}{2}$ | D. | h=$\frac{H}{4}$ |
10. 据新华社2015年11月2日上海电,我国自主发射的火星探测器将在第17届中国国际工业博览会上首次公开亮相.据介绍,我国自主火星探测的任务将通过一次发射,完成火星全球综合遥感和着陆巡视勘察两项探测任务.因此,火星探测器也分为“环绕器”与“着陆器”两个部分.若探测器从地面发射经过漫长飞行最终进入火星近地轨道进行全球综合遥感探测,然后“环绕器”与“着陆器”分离,着陆器进行着陆巡视勘察,关于火星探测器下列说法正确的是( )
据新华社2015年11月2日上海电,我国自主发射的火星探测器将在第17届中国国际工业博览会上首次公开亮相.据介绍,我国自主火星探测的任务将通过一次发射,完成火星全球综合遥感和着陆巡视勘察两项探测任务.因此,火星探测器也分为“环绕器”与“着陆器”两个部分.若探测器从地面发射经过漫长飞行最终进入火星近地轨道进行全球综合遥感探测,然后“环绕器”与“着陆器”分离,着陆器进行着陆巡视勘察,关于火星探测器下列说法正确的是( )
 据新华社2015年11月2日上海电,我国自主发射的火星探测器将在第17届中国国际工业博览会上首次公开亮相.据介绍,我国自主火星探测的任务将通过一次发射,完成火星全球综合遥感和着陆巡视勘察两项探测任务.因此,火星探测器也分为“环绕器”与“着陆器”两个部分.若探测器从地面发射经过漫长飞行最终进入火星近地轨道进行全球综合遥感探测,然后“环绕器”与“着陆器”分离,着陆器进行着陆巡视勘察,关于火星探测器下列说法正确的是( )
据新华社2015年11月2日上海电,我国自主发射的火星探测器将在第17届中国国际工业博览会上首次公开亮相.据介绍,我国自主火星探测的任务将通过一次发射,完成火星全球综合遥感和着陆巡视勘察两项探测任务.因此,火星探测器也分为“环绕器”与“着陆器”两个部分.若探测器从地面发射经过漫长飞行最终进入火星近地轨道进行全球综合遥感探测,然后“环绕器”与“着陆器”分离,着陆器进行着陆巡视勘察,关于火星探测器下列说法正确的是( )| A. | 火星探测器的发射速度应达到16.7km/s | |
| B. | 若测得探测器在火星近地轨道的环绕周期T及万有引力常量G,则可求火星的质量 | |
| C. | 若测得探测器在火星近地轨道的环绕周期T及万有引力常量G,则可求出火星的密度 | |
| D. | “环绕器”与“着陆器”分离后应点火减速实现变轨着陆 |
11.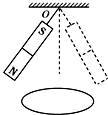 如图所示,条形磁铁用细线悬挂在O点,O点正下方固定一个水平放置的铝线圈.让磁铁在竖直面内摆动,下列说法中正确的是( )
如图所示,条形磁铁用细线悬挂在O点,O点正下方固定一个水平放置的铝线圈.让磁铁在竖直面内摆动,下列说法中正确的是( )
 如图所示,条形磁铁用细线悬挂在O点,O点正下方固定一个水平放置的铝线圈.让磁铁在竖直面内摆动,下列说法中正确的是( )
如图所示,条形磁铁用细线悬挂在O点,O点正下方固定一个水平放置的铝线圈.让磁铁在竖直面内摆动,下列说法中正确的是( )| A. | 磁铁摆动一个周期内,线圈内感应电流的方向改变4次 | |
| B. | 磁铁始终受到感应电流磁场的斥力作用 | |
| C. | 磁铁所受到的感应电流对它的作用力始终是阻力 | |
| D. | 磁铁所受到的感应电流对它的作用力有时是阻力有时是动力 |
 如图所示,在磁感应强度为B、足够大的水平匀强磁场中,有两块长为2L,间距为d的竖直放置的平行带电金属板,从CD板的正中央O点由静止释放一个初速为零的电子,电子恰好从AB板的边缘A端平行于AB板射出,且能回到O点.已知电子的电荷量为e,质量为m,重力可忽略不计,电场只局限于平行板之间,且L>d.
如图所示,在磁感应强度为B、足够大的水平匀强磁场中,有两块长为2L,间距为d的竖直放置的平行带电金属板,从CD板的正中央O点由静止释放一个初速为零的电子,电子恰好从AB板的边缘A端平行于AB板射出,且能回到O点.已知电子的电荷量为e,质量为m,重力可忽略不计,电场只局限于平行板之间,且L>d. 质量为2kg、长度为2.5m的长木板B在光滑的水平地面上以4m/s的速度向右运动,将一可视为质点的物体A轻放在B的右端,若A与B之间的动摩擦因数为0.2,A的质量为m=1kg.g=10m/s2,求
质量为2kg、长度为2.5m的长木板B在光滑的水平地面上以4m/s的速度向右运动,将一可视为质点的物体A轻放在B的右端,若A与B之间的动摩擦因数为0.2,A的质量为m=1kg.g=10m/s2,求