题目内容
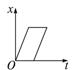
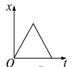
论述题：已知在匀速直线运动中，物体的位移对应v-t图象中的面积（如图a所示）．那么，对于做变速直线运动（图b所示）的物体，它在0～t时间内的位移能不能用v-t图象的面积表示？说明具体的证明过程．
解：在匀速直线运动中，物体的位移x=vt，v相当于图a中矩形的高度，t相当于矩形的长度，所以对应v-t图象中的面积表示位移．
那么，对于做变速直线运动（图b所示）的物体，
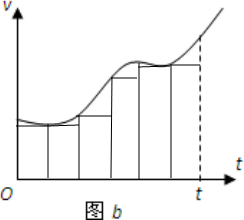
先把物体的运动分成几个小段，例如
算一个小段，每一小段相当于做匀速直线运动，我们可以用每一段的速度乘以的时间间隔，近似的当做各小段中物体的位移，在速度-时间图象中，各段位移可以用一个小矩形的面积代表，6个小矩形的面积之和近似的代表物体在整个过程中的位移．
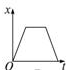
当然上面的做法是粗糙的，为了精确一些，可以把运动过程划分为更多的小段，如图所示：
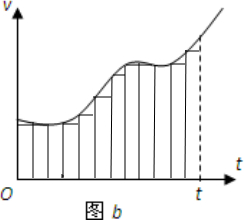
用所有这些小段的位移之和，近似的表示物体在整个过程的位移．从速度-时间图象上看，就是用更多的但是更窄的小矩形的面积之和代表物体的位移．
可以想象，如果把整个运动过程划分的非常非常细，很多很多小矩形的面积之和就能非常准确的代表物体的位移了．
分析：先把物体的变速运动分成几个小段，每一小段相当于做匀速直线运动，我们可以用每一段的速度乘以时间间隔，近似的当做各小段中物体的位移，在速度-时间图象中，各段位移可以用一个小矩形的面积代表，所有小矩形的面积之和近似的代表物体在整个过程中的位移．
点评：注意本题应用了极限思想，当把整个运动等分成无数份时，每一份的运动都可以看出匀速运动，然后应用求和的办法把所有面积相加．
那么，对于做变速直线运动（图b所示）的物体，
先把物体的运动分成几个小段，例如
算一个小段，每一小段相当于做匀速直线运动，我们可以用每一段的速度乘以的时间间隔，近似的当做各小段中物体的位移，在速度-时间图象中，各段位移可以用一个小矩形的面积代表，6个小矩形的面积之和近似的代表物体在整个过程中的位移．当然上面的做法是粗糙的，为了精确一些，可以把运动过程划分为更多的小段，如图所示：
用所有这些小段的位移之和，近似的表示物体在整个过程的位移．从速度-时间图象上看，就是用更多的但是更窄的小矩形的面积之和代表物体的位移．
可以想象，如果把整个运动过程划分的非常非常细，很多很多小矩形的面积之和就能非常准确的代表物体的位移了．
分析：先把物体的变速运动分成几个小段，每一小段相当于做匀速直线运动，我们可以用每一段的速度乘以时间间隔，近似的当做各小段中物体的位移，在速度-时间图象中，各段位移可以用一个小矩形的面积代表，所有小矩形的面积之和近似的代表物体在整个过程中的位移．
点评：注意本题应用了极限思想，当把整个运动等分成无数份时，每一份的运动都可以看出匀速运动，然后应用求和的办法把所有面积相加．
练习册系列答案
相关题目
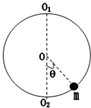有一种玩具结构如图所示，竖直放置的光滑铁圆环的半径为R=20cm，环上穿有一个带孔的小球m，仅能沿环做无摩擦滑动．如果圆环绕着通过环心的竖直轴O1O2以10rad/s的角速度旋转（g=10m/s2），则小球相对环静止时和环心O的连线与O1O2的夹角θ是
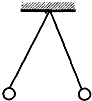如图所示，用两根等长的细线各悬一个小球，并挂于同一点，已知两球质量相等，当它们带上同种电荷时，相距r而平衡，若它们的电荷量都减少一半，待它们重新平衡后，两球的距离将