题目内容
15. 如图所示的“S”字形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成,固定在竖直平面内,轨道弯曲部分是由两个半径相等半圆连接而成,圆半径比细管内径大得多,轨道底端与水平地面相切,弹射装置将一个小球(可视为质点)从a点水平弹射向b点并进入轨道,经过轨道后从P点水平抛出,已知小物体与地面ab段间的动摩擦因数μ=0.2,不计其它机械能损失,ab段长L=1.25m,圆的半径R=0.1m,小物体质量m=0.01kg,轨道总质量为M=0.15kg,g=10m/s2,求:
如图所示的“S”字形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成,固定在竖直平面内,轨道弯曲部分是由两个半径相等半圆连接而成,圆半径比细管内径大得多,轨道底端与水平地面相切,弹射装置将一个小球(可视为质点)从a点水平弹射向b点并进入轨道,经过轨道后从P点水平抛出,已知小物体与地面ab段间的动摩擦因数μ=0.2,不计其它机械能损失,ab段长L=1.25m,圆的半径R=0.1m,小物体质量m=0.01kg,轨道总质量为M=0.15kg,g=10m/s2,求:(1)若v0=5m/s,小物体从P点抛出后的水平射程;
(2)设小球进入轨道之前,轨道对地面的压力大小等于轨道自身的重力,当v0至少为多少时,轨道对地面的压力为零.
分析 (1)对a到p运用动能定理求出小球到达P点的速度,根据平抛运动的规律求出小物体抛出后的水平射程.
(2)当小球在“S”形道中间位置轨道对地面的压力为零,此时速度最小,根据动能定理,结合牛顿第二定律求出最小的速度.
解答 解:(1)设小物体运动到p点的速度大小为v,对小物体由a点运动到p点过程,
由动能定理得:-μmgL-mg•4R=$\frac{1}{2}$mv2-$\frac{1}{2}$mvB2,
小物体离开P点后做平抛运动:
竖直方向:4R=$\frac{1}{2}$gt2,
水平方向:s=vt,
代入数据解得:s=0.4$\sqrt{6}$m;
(3)要使小球以最小速度v0运动,且轨道对地面的压力为零,则小球的位移应该在“S”形道中间位置.
根据牛顿第二定律得:F+mg=m$\frac{{v}_{1}^{2}}{R}$,由题意粒子:F=Mg,
根据动能定理得,-μmgL-mg•2R=$\frac{1}{2}$mv12-$\frac{1}{2}$mv02,
代入数据解得:v0=5m/s.
答:(1)小物体从P点抛出后的水平射程为0.4$\sqrt{6}$m.
(2)当v0=5m/s,轨道对地面的压力为零.
点评 本题综合考查牛顿第二定律和动能定理的运用,难度中等,涉及到圆周运动,平抛运动,需加强这方面题型的训练.

练习册系列答案
相关题目
7. 如图所示,一个电荷量为-Q的点电荷甲,固定在绝缘水平面上的O点.另一个电量为+q、质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲运动,到B点时的速度为v.且为运动过程中速度的最小值.已知点电荷乙与水平面的动摩擦因数为μ,AB间距离为L0,静电力常量为k,则下列说法正确的是( )
如图所示,一个电荷量为-Q的点电荷甲,固定在绝缘水平面上的O点.另一个电量为+q、质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲运动,到B点时的速度为v.且为运动过程中速度的最小值.已知点电荷乙与水平面的动摩擦因数为μ,AB间距离为L0,静电力常量为k,则下列说法正确的是( )
 如图所示,一个电荷量为-Q的点电荷甲,固定在绝缘水平面上的O点.另一个电量为+q、质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲运动,到B点时的速度为v.且为运动过程中速度的最小值.已知点电荷乙与水平面的动摩擦因数为μ,AB间距离为L0,静电力常量为k,则下列说法正确的是( )
如图所示,一个电荷量为-Q的点电荷甲,固定在绝缘水平面上的O点.另一个电量为+q、质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲运动,到B点时的速度为v.且为运动过程中速度的最小值.已知点电荷乙与水平面的动摩擦因数为μ,AB间距离为L0,静电力常量为k,则下列说法正确的是( )| A. | 点电荷乙从A点运动到B点的过程中,加速度先变大后变小 | |
| B. | OB间的距离为$\sqrt{\frac{kOq}{μmg}}$ | |
| C. | 点电荷乙能越过B点向左运动,其电势能增多 | |
| D. | 在点电荷甲形成的电场中,AB间电势差UAB=$\frac{μmg{L}_{0}+\frac{1}{2}m{v}^{2}-\frac{1}{2}m{v}_{0}^{2}}{q}$ |
3. 如图所示,条形磁铁静止在水平桌面上,闭合铝环从条形磁铁的正上方附近由静止竖直下落至桌面.则在下落过程中( )
如图所示,条形磁铁静止在水平桌面上,闭合铝环从条形磁铁的正上方附近由静止竖直下落至桌面.则在下落过程中( )
 如图所示,条形磁铁静止在水平桌面上,闭合铝环从条形磁铁的正上方附近由静止竖直下落至桌面.则在下落过程中( )
如图所示,条形磁铁静止在水平桌面上,闭合铝环从条形磁铁的正上方附近由静止竖直下落至桌面.则在下落过程中( )| A. | 下落过程中铝环能产生方向改变的感应电流 | |
| B. | 磁铁对桌面的压力始终大于其自身的重力 | |
| C. | 铝环所受安培力的方向先向上后向下 | |
| D. | 铝环的加速度小于或等于g |
20.用于加速粒子的回旋加速器其核心部分如图所示,两D形盒分别与电源相连.下列说法正确的是( )

| A. | 质子仅由电场加速 | |
| B. | 质子在电场中被加速,加速电压越高,射出的速率v越大 | |
| C. | D型盒的直径越大,射出的率度v越大 | |
| D. | 质子在磁场中运动的周期随质子速度增大而增大 |
7. 如图所示,在真空中,把一个绝缘导体向带负电的球P慢慢靠近.关于绝缘导体两端的电荷,下列说法中正确的是( )
如图所示,在真空中,把一个绝缘导体向带负电的球P慢慢靠近.关于绝缘导体两端的电荷,下列说法中正确的是( )
 如图所示,在真空中,把一个绝缘导体向带负电的球P慢慢靠近.关于绝缘导体两端的电荷,下列说法中正确的是( )
如图所示,在真空中,把一个绝缘导体向带负电的球P慢慢靠近.关于绝缘导体两端的电荷,下列说法中正确的是( )| A. | 两端的感应电荷越来越少 | B. | 两端的感应电荷是同种电荷 | ||
| C. | 两端的感应电荷是异种电荷 | D. | 两端的感应电荷电荷量相等 |
5.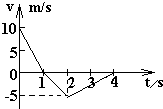 一个质量为1kg的物体在水平恒力F作用下沿水平面运动,一段时间后撤去F,该物体运动的v-t图象,如图所示,(g=10m/s2),则下列说法正确的是( )
一个质量为1kg的物体在水平恒力F作用下沿水平面运动,一段时间后撤去F,该物体运动的v-t图象,如图所示,(g=10m/s2),则下列说法正确的是( )
 一个质量为1kg的物体在水平恒力F作用下沿水平面运动,一段时间后撤去F,该物体运动的v-t图象,如图所示,(g=10m/s2),则下列说法正确的是( )
一个质量为1kg的物体在水平恒力F作用下沿水平面运动,一段时间后撤去F,该物体运动的v-t图象,如图所示,(g=10m/s2),则下列说法正确的是( )| A. | 物体2s末距离出发点最远 | B. | 拉力F的方向与初速度方向相反 | ||
| C. | 拉力在1s末撤去的 | D. | 摩擦力大小为10N |
 如图所示,用细线OA、0B悬挂一重物,OA和OB与天花板的夹角分别为θ1=30°和θ2=60,它们所能承受的最大拉力分别为F1=1000N和F2=1500N,求悬挂物的最大重力.
如图所示,用细线OA、0B悬挂一重物,OA和OB与天花板的夹角分别为θ1=30°和θ2=60,它们所能承受的最大拉力分别为F1=1000N和F2=1500N,求悬挂物的最大重力. 如图所示,在竖直平面内的直角坐标系xoy中,第Ⅳ象限内存在沿x轴负方向的匀强电场.一质量为m、电量为q的带正电小球从x轴上的A点由静止释放,打在y轴上的B点.已知A点坐标为(2l,0),B点坐标为(0,-l).求:
如图所示,在竖直平面内的直角坐标系xoy中,第Ⅳ象限内存在沿x轴负方向的匀强电场.一质量为m、电量为q的带正电小球从x轴上的A点由静止释放,打在y轴上的B点.已知A点坐标为(2l,0),B点坐标为(0,-l).求: