题目内容
6．
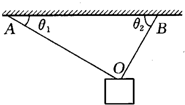如图所示，用细线OA、0B悬挂一重物，OA和OB与天花板的夹角分别为θ1=30°和θ2=60，它们所能承受的最大拉力分别为F1=1000N和F2=1500N，求悬挂物的最大重力．
分析 以结点C为研究对象作出受力分析图，分析BC、AC两绳拉力的大小，确定哪根绳子的拉力先达到最大．再根据受力平衡列方程解得结果．
解答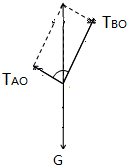 
解：分析结点O的受力图如图，运用合成法，由几何知识：
TBO=TAOtan60°
若TAO=F1=1000N，
则得：TBO=1000$\sqrt{3}$N＞F2=1500N
可知，当悬挂物的重力逐渐增大时，BO细线的拉力先达到最大值，将被拉断，则当TBO=F2=1500N时，有：
G=$\frac{{T}_{BO}}{sin60°}$=$\frac{1500}{\frac{\sqrt{3}}{2}}$N=1000$\sqrt{3}$N
答：悬挂物的最大重力是1000$\sqrt{3}$N．
点评 本题是静力学中临界问题，分析临界条件是关键．当绳子刚要被拉断时，绳子的拉力达到最大值，是常用的临界条件．
练习册系列答案
相关题目
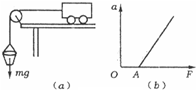如图中（a）所示是“探究质量一定的物体加速度与作用力的关系”实验装置．研究对象是放在长木板上的小车，小车的质量为m，长木板水平放置，小车前端拴着细轻绳，跨过定滑轮，下面吊着砂桶，当砂和桶总质量远小于（填“等于”、“远大于”或“远小于”）小车质量时，可认为细绳对小车的作用力等于砂和桶的总重力mg，用改变砂子质量的办法，来改变对小车的作用力F，用打点计时器测出小车的加速度a，得出若干组F和a的数据，画出a-F图线（如图（b）所示）．分析这一图线，直线明显没有通过原点，这不符合牛顿第二定律的a和F的正比关系，这是因为在实验中未平衡摩擦力或平衡不足．实验中平衡摩擦力时应稍微抬高木板无滑轮端使得不挂砂桶（选填“挂砂桶”或“不挂砂桶”）的小车在木板上匀速下行．
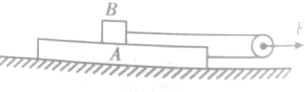总质量为M的两物块A、B静止叠放在水平面上上，用轻绳通过滑轮将A、B连接，A与B及水平面间的动摩擦因数均为μ，对滑轮轴施加一个水平力F，如图所示：
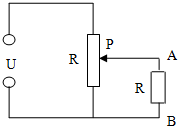如图所示，是将滑动变阻器作分压器用的电路，A、B为分压器的输出端，滑动变阻器的总阻值为R，负载电阻的阻值也是R，电源电压为U保持恒定．求：
1．质量为m的木块置于水平地面上，木块在与水平方向成θ角向上的拉力F作用下沿地面做匀速直线运动，则木块所受地面的摩擦力大小为（ ）
| A． | F | B． | Fcosθ | C． | Fsinθ | D． | μmg |
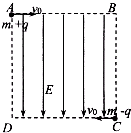如图所示，在边长为L的正方形区域ABCD内，存在沿AD方向的匀强电场，质量均为m，带电量分别为+q和-q的两粒子，同时由A、C两点沿AB和CD方向以速率v0进入正方形区域，两粒子在区域的正中心相遇．若将区域中的电场换为垂直纸面向外的匀强磁场，两粒子同时由A、B两点沿平行于AB方向进入区域，速度大小仍为v0，两粒子也在区域的正中心相遇，不计粒子的重力和粒子间的相互作用力，求：
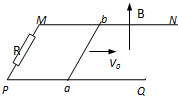如图所示，水平面上有两根相距0.5m的足够长的光滑平行金属导轨MN和PQ，它们的电阻可忽略不计，在M和P之间接有阻值为R=3.0Ω的定值电阻．导体棒ab长l=0.5m，质量m=1kg，其电阻为r=1.0Ω，与导轨接触良好．整个装置处于方向竖直向上的匀强磁场中，磁感应强度B=0.4T．现使ab以v0=10m/s的速度向右做匀速运动．
如图所示的“S”字形玩具轨道，该轨道是用内壁光滑的薄壁细圆管弯成，固定在竖直平面内，轨道弯曲部分是由两个半径相等半圆连接而成，圆半径比细管内径大得多，轨道底端与水平地面相切，弹射装置将一个小球（可视为质点）从a点水平弹射向b点并进入轨道，经过轨道后从P点水平抛出，已知小物体与地面ab段间的动摩擦因数μ=0.2，不计其它机械能损失，ab段长L=1.25m，圆的半径R=0.1m，小物体质量m=0.01kg，轨道总质量为M=0.15kg，g=10m/s2，求：