Question

（2011?保定模拟）如图所示，用三根轻绳AB、BC、CD连接两个小球，两球质量均为m，A、D两端固定，系统在竖直平面内静止，AB和CD与竖直方向的夹角分别是30°和60°．则（　　）

• A．AB拉力是

  3

  mg
• B．BC拉力是mg
• C．CD拉力是mg
• D．BC与水平方向夹角是60°

Answer 1

分析：先对BC球整体受力分析，根据共点力平衡条件，运用合成法求解AB绳拉力和CD绳子拉力，再对C球受力分析，结合共点力平衡条件再次列式求解．

解答：解：对BC球整体受力分析，如图


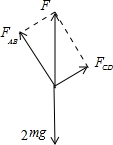
根据共点力平衡条件，有
F_AB=2mg?cos30°=

3

mg
F_CD=2mg?sin30°=mg
再对C球受力分析，如图

根据共点力平衡条件，有
x方向：F_CDcos30°-F_BCcosα=0
y方向：F_CDsin30°+F_BCsinα-mg=0
解得
F_BC=mg
α=30°
故选ABC．

点评：整体法与隔离法是解决平衡问题的常用方法，在具体问题中，灵活地选用整体法和隔离法，可以使问题大大简化．