题目内容
1.一条船在静水中的速度为3m/s,它要横渡一条宽为30m的河,河中水流速度为4m/s,则此船( )| A. | 不可能垂直于河岸抵达正对岸 | B. | 船对地速度大小一定为5m/s | ||
| C. | 渡河最短时间为6s | D. | 渡河的时间可能为8.5s |
分析 船既随水向下游运动,又相对于水向对岸行驶,根据船相对于水的速度与水流速度的比较,分析船能否到达正对岸.假设船头的指向与河岸的夹角为α,运用速度的分解求出船垂直于河岸方向的分速度,分析什么条件时渡河的时间最短,并进行求解.
解答 解:设船在静水中的航速为v1,水流的速度v2.
A、由题,船在静水中的航速小于水流的速度,根据平行四边形定则可知,船的合速度方向不可能垂直于河岸,则 船不能垂直到达正对岸,故A正确;
船不能垂直到达正对岸,故A正确;
B、当船速垂直河岸行驶时,船对地速度大小才为5m/s,故B错误;
CD、将小船的速度分解为垂直河岸和沿河岸方向,在垂直于河岸的方向上,河宽一定,当在该方向上的速度最大时,渡河时间最短,所以当船头方向垂直河岸,在该方向上的速度等于静水船速,时间最短,为t=$\frac{d}{{v}_{1}}$=10s.故CD错误;
故选:A.
点评 本题是小船渡河问题,关键是运用运动的合成与分解做出速度分解或合成图,分析最短时间或最短位移渡河的条件.

练习册系列答案
相关题目
11.如果在某电场中将5.0×10-8C的电荷由A点移到B点,电场力做功为6.0×10-3J,那么( )
| A. | A、B两点间的电势差是1.2×105V | |
| B. | A、B两点间的电势差是3.0×10-10V | |
| C. | 若在A、B两点间移动2.5×10-8C的电荷,电场力将做7.5×10-18J的功 | |
| D. | 若在A、B两点间移动1.0×10-7C的电荷,电场力将做3.0×10-17J的功 |
11.关于加速度,下列说法中正确的是( )
| A. | 速度大,加速度必定也大 | |
| B. | 加速度的方向和速度方向一定相同 | |
| C. | 加速度越大,表示物体的速度变化越大 | |
| D. | 加速度越大,表示物体的速度变化越快 |
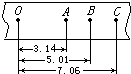 在“验证机械能守恒定律”的实验中,打点计时器接在电压为 6V频率为50Hz的交流电源上,自由下落的重物质量为1kg,一条理想的纸带,数据如图所示,单位是cm,g取9.8m/s2,O、A之间有几个计数点没画出.
在“验证机械能守恒定律”的实验中,打点计时器接在电压为 6V频率为50Hz的交流电源上,自由下落的重物质量为1kg,一条理想的纸带,数据如图所示,单位是cm,g取9.8m/s2,O、A之间有几个计数点没画出.
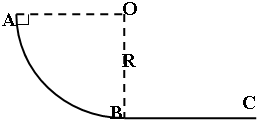 如图所示:小物体从半径为R的四分之一光滑竖直圆弧轨道顶端A由静止下滑后,在粗糙水平面BC上又滑行了一段s停止,图中OA线水平,OB线竖直,O是圆心.则:
如图所示:小物体从半径为R的四分之一光滑竖直圆弧轨道顶端A由静止下滑后,在粗糙水平面BC上又滑行了一段s停止,图中OA线水平,OB线竖直,O是圆心.则: 在测量金属丝电阻率的实验中:
在测量金属丝电阻率的实验中: 如图所示,A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,A、B、C三点的半径分别为RA、RB、RC,角速度分别为ωA、ωB、ωC,它们之间靠摩擦传动,接触面上没有滑动.若ωB:ωC=4:1,则ωA:ωB=1:4,RA:RB:RC=4:1:2.
如图所示,A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,A、B、C三点的半径分别为RA、RB、RC,角速度分别为ωA、ωB、ωC,它们之间靠摩擦传动,接触面上没有滑动.若ωB:ωC=4:1,则ωA:ωB=1:4,RA:RB:RC=4:1:2.