题目内容
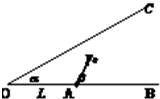 如图所示,在水平面OB上有一A点,已知OA=L.现在从A点以初速度v0射出一小球,在不被倾角为α(α<45°)的OC面板弹回的前提下,问:
如图所示,在水平面OB上有一A点,已知OA=L.现在从A点以初速度v0射出一小球,在不被倾角为α(α<45°)的OC面板弹回的前提下,问:(1)若小球射出时的角度θ=45°,为使得小球能射到最远,小球射出时的初速度v0应为多大?
(2)若小球射出时的初速度v0已知,且大于第(1)小题中所得的结果,为使小球能射到最远,小球射出时的角度θ应为多大?
分析:(1)小球做斜抛运动,轨迹为抛物线,要使小球能射到最远,小球轨迹与直线OC相切,故将抛物线方程与直线方程联立方程组后,方程组只有一个解,据此求初速度的值.
(2)与上问同理,整理可得小球射出时的角度θ
(2)与上问同理,整理可得小球射出时的角度θ
解答:解:(1)以A点为坐标原点,AB方向为x轴正方向建立坐标系,小球做斜抛运动,坐标为:
x=v0tcosθ,y=v0tsinθ-
gt2,
代入得:y=xtanθ-
,
OC线方程:y=(x+L)tanα,
联立可得:xtanθ-
=(x+L)tanα,
取θ=45°,得:
+(tanα-1)x+Ltanα=0,
为使小球以45°抛出能实现射程最远而不被OC面板弹回,小球抛射轨迹应与斜面OC相切,即方程只有一个解,
即:△=(tanα-1)2-
tanα=0,
解得:v0=
,
(2)当v0>
时,以A点为坐标原点,AB方向为x轴正方向建立坐标系,小球做斜抛运动,坐标为:x=v0tcosθ,y=v0tsinθ-
gt2,
代入得:y=xtanθ-
,
OC线方程:y=(x+L)tanα,
联立可得:xtanθ-
=(x+L)tanα,
为使小球以θ角抛出能实现射程最远而不被OC面弹回,必有θ>α,小球抛射轨迹应与斜面OC相切,可得判别式:△=(tanα-tanθ)2-
tanα=0,
即sin2(α-θ)-
sin2α=0,
因为θ>α,所以θ=α+sin-1
.
答:(1)小球射出时的初速度v0应为
,
(2)小球射出时的角度θ应为α+sin-1
.
x=v0tcosθ,y=v0tsinθ-
| 1 |
| 2 |
代入得:y=xtanθ-
| gx2 | ||
|
OC线方程:y=(x+L)tanα,
联立可得:xtanθ-
| gx2 | ||
|
取θ=45°,得:
| gx2 | ||
|
为使小球以45°抛出能实现射程最远而不被OC面板弹回,小球抛射轨迹应与斜面OC相切,即方程只有一个解,
即:△=(tanα-1)2-
| 4gL | ||
|
解得:v0=
|
(2)当v0>
|
| 1 |
| 2 |
代入得:y=xtanθ-
| gx2 | ||
|
OC线方程:y=(x+L)tanα,
联立可得:xtanθ-
| gx2 | ||
|
为使小球以θ角抛出能实现射程最远而不被OC面弹回,必有θ>α,小球抛射轨迹应与斜面OC相切,可得判别式:△=(tanα-tanθ)2-
| 4gL | ||
|
即sin2(α-θ)-
| gL | ||
|
因为θ>α,所以θ=α+sin-1
| ||
| v0 |
答:(1)小球射出时的初速度v0应为
|
(2)小球射出时的角度θ应为α+sin-1
| ||
| v0 |
点评:关键是:能够挖掘出“不被倾角为α(α<45°)的OC面板弹回”的隐含信息为小球抛射轨迹应与斜面OC相切;能进行三角函数变换

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
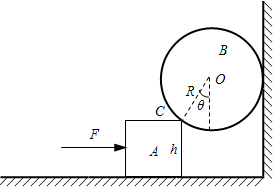 (2011?南通二模)如图所示,在水平面和竖直墙壁之间放置质量为m,高为h的木块A和质量为M、半径为R的球B,各接触面均光滑,木块A受到水平向右的外力F的作用,系统处于静止状态.O为B的球心,C为A、B接触点,CO与竖直方向夹角θ=60°.现撤去水平外力F,则( )
(2011?南通二模)如图所示,在水平面和竖直墙壁之间放置质量为m,高为h的木块A和质量为M、半径为R的球B,各接触面均光滑,木块A受到水平向右的外力F的作用,系统处于静止状态.O为B的球心,C为A、B接触点,CO与竖直方向夹角θ=60°.现撤去水平外力F,则( )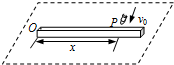 如图所示,在水平面内有一质量分布均匀的木杆可绕端点O在水平面上自由转动.一颗子弹以垂直于杆的水平速度v0击中静止木杆上的P点,并随木杆一起转动.已知木杆质量为M,长度为L;子弹质量为m,点P到点O的距离为x.忽略木杆与水平面间的摩擦.设子弹击中木杆后绕点O转动的角速度为ω.下面给出ω的四个表达式中只有一个是合理的.根据你的判断,ω的合理表达式应为( )
如图所示,在水平面内有一质量分布均匀的木杆可绕端点O在水平面上自由转动.一颗子弹以垂直于杆的水平速度v0击中静止木杆上的P点,并随木杆一起转动.已知木杆质量为M,长度为L;子弹质量为m,点P到点O的距离为x.忽略木杆与水平面间的摩擦.设子弹击中木杆后绕点O转动的角速度为ω.下面给出ω的四个表达式中只有一个是合理的.根据你的判断,ω的合理表达式应为( ) 如图所示,在水平面直线MN的上方有一方向与MN成30°角的斜向右下方的匀强电场,电场区域足够宽,场强大小为E.在MN下方有一半径为R的圆形区域,圆心为O,圆O与MN相切于D点,圆形区域内分布有垂直纸面向里的匀强磁场.在MN上有一点C,圆心O与C点的连线和电场线平行,在OC的延长线上有一点P,P点到边界MN的垂直距离为0.5R.一质量为m、电荷量为q的带正电的粒子从P点静止释放.已知圆形磁场的磁感应强度大小为
如图所示,在水平面直线MN的上方有一方向与MN成30°角的斜向右下方的匀强电场,电场区域足够宽,场强大小为E.在MN下方有一半径为R的圆形区域,圆心为O,圆O与MN相切于D点,圆形区域内分布有垂直纸面向里的匀强磁场.在MN上有一点C,圆心O与C点的连线和电场线平行,在OC的延长线上有一点P,P点到边界MN的垂直距离为0.5R.一质量为m、电荷量为q的带正电的粒子从P点静止释放.已知圆形磁场的磁感应强度大小为 如图所示,在水平面和竖直墙壁之间放置质量为m、高为h的木块A和质量为M、半径为R的球B,各接触面均光滑,木块A受到水平向右的外力F作用,系统处于静止状态.O为B的球心,C为A、B接触点,CO与竖直方向夹角为θ=600.现撤去水平外力F,则( )
如图所示,在水平面和竖直墙壁之间放置质量为m、高为h的木块A和质量为M、半径为R的球B,各接触面均光滑,木块A受到水平向右的外力F作用,系统处于静止状态.O为B的球心,C为A、B接触点,CO与竖直方向夹角为θ=600.现撤去水平外力F,则( )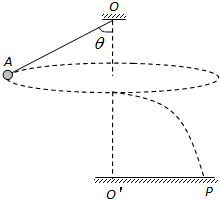 如图所示,在水平面内做匀速圆周运动的圆锥摆,O为悬点,O′为O在水平地面上的投影,已知绳长为a,绳与竖直方向夹角为θ=60°,OO′间距离为
如图所示,在水平面内做匀速圆周运动的圆锥摆,O为悬点,O′为O在水平地面上的投影,已知绳长为a,绳与竖直方向夹角为θ=60°,OO′间距离为