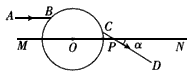题目内容
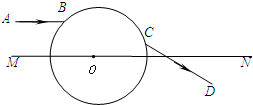 如图所示,一透明球体置于空气中,球半径R=10cm,折射率n=
如图所示,一透明球体置于空气中,球半径R=10cm,折射率n=| 2 |
| 2 |
①完成光路;
②计算:光从B点传到C点的时间.
分析:根据入射光线和出射光线作出光路图,根据几何关系求出入射角的大小,通过折射定律求出折射角的大小,从而通过几何关系求出光在透明球体中运动的距离,根据v=
得出光在介质中的速度,从而求出光从B点传到C点的时间.
| c |
| n |
解答:解:①光路图如图所示.
②如图所示,光在介质中的传播速度v=
=
=
m/s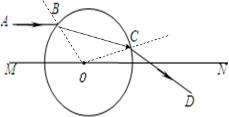
根据几何关系知,sini=
=
=
根据折射定律得,
=n
则折射角sinr=
,
解得r=30°
光线在玻璃砖中传播的距离为
s=2Rcos30°=10
cm,
因为s=vt
则t=
=
s=
×10-8s
答:①光路图如图所示.
②光从B点传到C点的时间为
×10-8s.
②如图所示,光在介质中的传播速度v=
| c |
| n |
| 3×108 | ||
|
3
| ||
| 2 |

根据几何关系知,sini=
| d |
| R |
5
| ||
| 10 |
| ||
| 2 |
根据折射定律得,
| sini |
| sinr |
则折射角sinr=
| 1 |
| 2 |
解得r=30°
光线在玻璃砖中传播的距离为
s=2Rcos30°=10
| 3 |
因为s=vt
则t=
| s |
| v |
0.1
| ||||
|
| ||
| 30 |
答:①光路图如图所示.
②光从B点传到C点的时间为
| ||
| 30 |
点评:本题考查光的折射定律的基本运用,对数学几何能力的要求较高,需加强这方面的训练.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

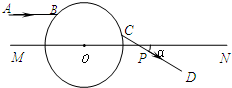
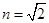 , MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B点为入射点,AB与MN间距为
, MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B点为入射点,AB与MN间距为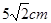 ,CD为出射光线,与MN交于P点。(已知光在真空中的速度
,CD为出射光线,与MN交于P点。(已知光在真空中的速度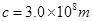 )。求:
)。求: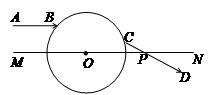
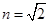 ,
MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B点为入射点,AB与MN间距为
,
MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B点为入射点,AB与MN间距为 ,CD为出射光线,与MN交于P点。(已知光在真空中的速度
,CD为出射光线,与MN交于P点。(已知光在真空中的速度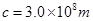 )。求:
)。求: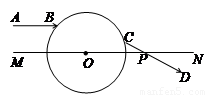
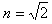 ,MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN的间距为
,MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN的间距为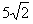 cm,CD为出射光线。求CD与MN所成的角α的大小。
cm,CD为出射光线。求CD与MN所成的角α的大小。