题目内容
(1)利用发波水槽得到的水面波形如a,b所示,则

A.图a、b均显示了波的干涉现象
B.图a、b均显示了波的衍射现象
C.图a显示了波的干涉现象,图b显示了波的衍射现象
D.图a显示了波的衍射现象,图b显示了波的干涉现象
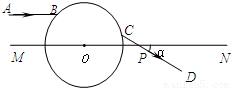
(2)如图所示,一透明球体置于空气中,球半径R=10cm,折射率n=
.MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5
cm,CD为出射光线.
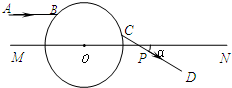
①补全光路并求出光从B点传到C点的时间;
②求CD与MN所成的角α.(需写出求解过程)
D
D

A.图a、b均显示了波的干涉现象
B.图a、b均显示了波的衍射现象
C.图a显示了波的干涉现象,图b显示了波的衍射现象
D.图a显示了波的衍射现象,图b显示了波的干涉现象
(2)如图所示,一透明球体置于空气中,球半径R=10cm,折射率n=
| 2 |
| 2 |

①补全光路并求出光从B点传到C点的时间;
②求CD与MN所成的角α.(需写出求解过程)
分析:(1)单缝能产生衍射现象,两列波频率相同时能产生干涉现象.
(2)①连接BC,作出光路图.根据几何知识求出光在球体内通过的距离和光的速度,再求出光从B点传到C点的时间;②根据几何知识求出α.
(2)①连接BC,作出光路图.根据几何知识求出光在球体内通过的距离和光的速度,再求出光从B点传到C点的时间;②根据几何知识求出α.
解答:解:
(1)a图是单缝,波绕单缝继续传播,产生了衍射现象.b图两个振子频率相同,产生了干涉现象.
故选D
(2)①连接BC,如图所示,
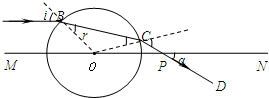
在B点光线的入射角、折射角分别标为i、r,
sini=
=
所以,i=45°
由折射率定律:
在B点有:n=
,sinr=
=
故:r=30°
由几何知识,BC=2Rcosr
光从B点传到C点的时间t=
=
=
=
代入解得t=
×10-9s
②根据光路的可逆性,由几何关系
可知∠COP=180°-i-(180°-2r)=15°
∠OCP=180°-r=180°-45°=135°
所以α=18O°-∠COP-∠OCP=30°
故答案为:
(1)D
(2)①光路如图.光从B点传到C点的时间为
×10-9s;
②CD与MN所成的角α=30°.
(1)a图是单缝,波绕单缝继续传播,产生了衍射现象.b图两个振子频率相同,产生了干涉现象.
故选D
(2)①连接BC,如图所示,

在B点光线的入射角、折射角分别标为i、r,
sini=
5
| ||
| 10 |
| ||
| 2 |
所以,i=45°
由折射率定律:
在B点有:n=
| sini |
| sinr |
| sini |
| n |
| 1 |
| 2 |
故:r=30°
由几何知识,BC=2Rcosr
光从B点传到C点的时间t=
| BC |
| v |
| BC | ||
|
| 2BC?n |
| c |
| 2nRcosr |
| c |
代入解得t=
| ||
| 6 |
②根据光路的可逆性,由几何关系
可知∠COP=180°-i-(180°-2r)=15°
∠OCP=180°-r=180°-45°=135°
所以α=18O°-∠COP-∠OCP=30°
故答案为:
(1)D
(2)①光路如图.光从B点传到C点的时间为
| ||
| 6 |
②CD与MN所成的角α=30°.
点评:本题是几何光学问题,是折射定律和几何知识的综合应用,作出光路图是解题的基础.

练习册系列答案
相关题目
 (2010?上海)利用发波水槽得到的水面波形如图a、b所示,则( )
(2010?上海)利用发波水槽得到的水面波形如图a、b所示,则( ) 利用发波水槽得到的水面波形如图a、b所示,则( )
利用发波水槽得到的水面波形如图a、b所示,则( )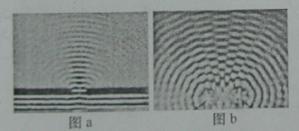


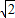 .MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5
.MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5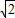 cm,CD为出射光线.
cm,CD为出射光线.