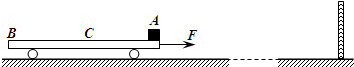题目内容
如图所示，平板车质量为m，长为L，车右端（A点）有一个质量为M=2m的小滑块（可视为质点）．平板车静止于光滑水平面上，小车右方足够远处固定着一竖直挡板，小滑块与车面间有摩擦，并且在AC段、CB段动摩擦因数不同，分别为μ1、μ2，C为AB的中点．现给车施加一个水平向右的恒力，使车向右运动，同时小物块相对于小车滑动，当小滑块滑至C点时，立即撤去这个力．已知撤去这个力的瞬间小滑块的速度为v，车的速度为2v，之后小滑块恰好停在车的左端（B点）与车共同向前运动，并与挡板发生无机械能损失的碰撞．试求：（1）μ1和μ2的比值．
（2）通过计算说明，平板车与挡板碰撞后，是否还能再次向右运动．
【答案】分析：（1）分别对滑块和小车运用进行受力分析，根据运动学公式和动量守恒定律进行计算求出动摩擦因数之比；
（2）对滑块和小车组成的系统运用动量守恒定律和能量守恒定律求解小车碰撞后滑块的运动，从而判断是否再次向右运动．
解答：解：设在有水平外力F时平板车的加速度为a1，在无水平外力F时平板车的加速度为a2，小滑块在AC段和CB段的加速度分别为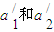
由牛顿第二定律得：μ1?2mg=2m?a'1解得：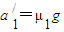
①
同理：
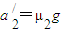②
当小滑块在AC段运动时，由题意可知：
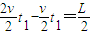③
④
由①③④联立得：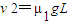
⑤
设小滑块滑到B端时与车的共同速度为v1，由于滑块从C滑到B的过程中，滑块和车的系统受到的合外力为零，故动量守恒，于是有：
2m?v+m?2v=（2m+m）v1⑥
当小滑块在在CB段运动时，由运动学知识可知：
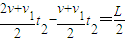
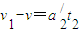⑧
由②⑥⑦⑧联立得：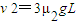
⑨
所以，由⑤⑨得：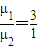
（2）设小滑块滑到B端时与车的共同速度为v1，由于滑块从C滑到B的过程中，滑块和车的系统受到的合外力为零，故动量守恒，于是有：
2m?v+m?2v=（2m+m）v1①
平板车与挡板碰撞后以原速大小返回，之后车向左减速，滑块向右减速，由于M=2m，所以车的速度先减小到零．设车向左运动的速度减小为零时，滑块的速度为v2，滑块滑离车B端的距离为L1．
由于上述过程系统的动量守恒，于是有：2m?v1-mv1=2m?v2②
对车和滑块的系统运用能量守恒定律得：
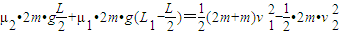③
由①②③式及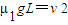
、
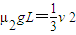
可解得：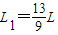
由于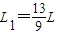
＞L，故小车的速度还没有减为零时，小物块已经从小车的右端滑下，之后小车向左匀速运动，故车不会再向右运动了
答：（1）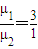
；
（2）平板车与挡板碰撞后，不再向右运动．
点评：本题综合运用了动能定理、动量定理、动量守恒定律以及能量守恒定律，属于较难题．运用这些规律解题时一定要合适地选择研究的过程．
（2）对滑块和小车组成的系统运用动量守恒定律和能量守恒定律求解小车碰撞后滑块的运动，从而判断是否再次向右运动．
解答：解：设在有水平外力F时平板车的加速度为a1，在无水平外力F时平板车的加速度为a2，小滑块在AC段和CB段的加速度分别为
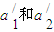
由牛顿第二定律得：μ1?2mg=2m?a'1解得：
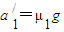①同理：
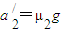②当小滑块在AC段运动时，由题意可知：
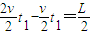③④由①③④联立得：
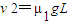⑤设小滑块滑到B端时与车的共同速度为v1，由于滑块从C滑到B的过程中，滑块和车的系统受到的合外力为零，故动量守恒，于是有：
2m?v+m?2v=（2m+m）v1⑥
当小滑块在在CB段运动时，由运动学知识可知：
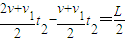
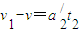⑧由②⑥⑦⑧联立得：
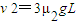⑨所以，由⑤⑨得：
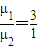
（2）设小滑块滑到B端时与车的共同速度为v1，由于滑块从C滑到B的过程中，滑块和车的系统受到的合外力为零，故动量守恒，于是有：
2m?v+m?2v=（2m+m）v1①
平板车与挡板碰撞后以原速大小返回，之后车向左减速，滑块向右减速，由于M=2m，所以车的速度先减小到零．设车向左运动的速度减小为零时，滑块的速度为v2，滑块滑离车B端的距离为L1．
由于上述过程系统的动量守恒，于是有：2m?v1-mv1=2m?v2②
对车和滑块的系统运用能量守恒定律得：
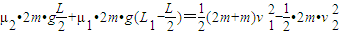③由①②③式及
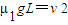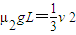
、可解得：
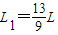
由于
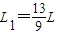＞L，故小车的速度还没有减为零时，小物块已经从小车的右端滑下，之后小车向左匀速运动，故车不会再向右运动了答：（1）
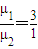；（2）平板车与挡板碰撞后，不再向右运动．
点评：本题综合运用了动能定理、动量定理、动量守恒定律以及能量守恒定律，属于较难题．运用这些规律解题时一定要合适地选择研究的过程．
练习册系列答案
相关题目
)．
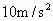