��Ŀ����
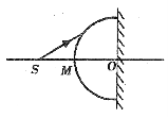
����Ŀ����14�֣���ͼ��ʾ���ڳ�ǿ��СΪE��������ֱ���ϵ���ǿ�糡��ȡһ���뾶ΪR��Բ�ܣ�Բ������ƽ��ƽ���ڵ糡����O��Ϊ��Բ�ܵ�Բ�ģ�A����Բ���ϵ���͵㣬B����Բ�������Ҳ�ĵ㡣��A���з���Դ����Բ�����ڵ�ƽ�������Ŵ�ֱ�糡���ҵķ����ͷų���ͬ�������ӣ���Щ���Ӵ�A�㷢��ʱ�ij��ٶȴ�С������ͬ����֪���ӵ�����Ϊm�������Ϊq������������

��1��ijһ�����˶��켣����Բ���ϵ�B�㣬������Ӵ�A�㷢��ʱ�ij��ٶȴ�С��
��2��ȡԲ���ϵ�C�㣬ʹOC������OA�н�Ϊ�ȣ���������Ӿ���C��ʱ�Ķ��ܱ���ʽ��
��3�����ڣ�2�����е�C��λ�������=60�㣬���BC֮�䴩��Բ�ܵ���Щ�����о���Բ��ʱ����õ�����ܺ���С���ֱܷ��Ƕ��٣�
���𰸡���1��![]() ��2��
��2��![]() qER(53cos��) ��3��
qER(53cos��) ��3��![]()
![]()
����������1����ɴ�A��B����ƽ���˶�����ţ�ٵڶ����ɵ�![]() ��1�֣�
��1�֣�
ˮƽ����R=v0t��1�֣�
��ֱ����R=![]() at2��1�֣�
at2��1�֣�
������ã�![]() ��1�֣�
��1�֣�
��2����ɴ�A��C����ƽ���˶������������֪
Rsin��=vt��1�֣�
![]() ��1�֣�
��1�֣�
![]() ��1�֣�
��1�֣�
���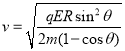 ��1�֣�
��1�֣�
�辭��C��ʱ�Ķ���ΪEk������ݶ��ܶ�����
qE(R�CRcos��)=Ek![]() mv2��1�֣�
mv2��1�֣�
���Ek=![]() qER(53cos��)��1�֣�
qER(53cos��)��1�֣�
��3���ɣ�2���ʵĽ��ۿ�֪��������0���仯��180�������Ӿ���Բ��ʱ�Ķ���������C����յ��ĵ�ɵ�ĩ������С��B����յ��ĵ�ɵ�ĩ�������
![]() ��2�֣�
��2�֣�
![]() ��2�֣�
��2�֣�