Question

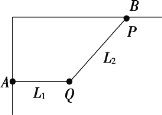
【题目】如图所示为一种获得高能粒子的装置原理图，环形管内存在垂直于纸面、磁感应强度大小可调的匀强磁场（环形管的宽度非常小），质量为m、电荷量为q的带正电粒子可在环中做半径为R的圆周运动。A、B为两块中心开有小孔且小孔距离很近的平行极板，原来电势均为零，每当带电粒子经过A板刚进入A、B之间时，A板电势升高到+U，B板电势仍保持为零，粒子在两板间的电场中得到加速，每当粒子离开B板时，A板电势又降为零，粒子在电场中一次一次地加速使得动能不断增大，而在环形区域内，通过调节磁感应强度大小可使粒子运行半径R不变。已知极板间距远小于R，则下列说法正确的是（　　）

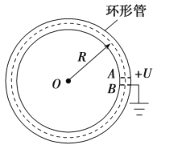
A.环形区域内匀强磁场的磁场方向垂直于纸面向里

B.粒子从A板小孔处由静止开始在电场力作用下加速，绕行N圈后回到A板时获得的总动能为2NqU

C.粒子在绕行的整个过程中，A板电势变化的周期不变

D.粒子绕行第N圈时，环形区域内匀强磁场的磁感应强度为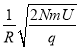

Answer 1

【答案】D

【解析】

A．正电荷在AB之间是加速，故电荷顺时针转动，在磁场中洛伦兹力提供向心力，所以磁场方向垂直于纸面向外，选项A错误；

B．粒子在电场中加速，根据动能定理有

选项B错误；

C．A板电势变化的周期与粒子在磁场中圆周运动的周期相同，由于粒子在加速速度增大，根据可知周期要递减，选项C错误；

D．粒子在电场中加速，由动能定理知

解得

粒子在磁场中由牛顿第二定律有

解得

选项D正确。

故选D。