题目内容
【题目】如图，斜面上有a、b、c、d四个点，ab=bc=cd，从a点以初速度v0水平抛出一个小球，它落在斜面上的b点，速度方向与斜面之间的夹角为θ；若小球从a点以初速度 
v0水平抛出，不计空气阻力，则小球（ ）
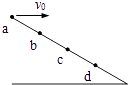
A.将落在bc之间
B.将落在c点
C.落在斜面的速度方向与斜面的夹角大于θ
D.落在斜面的速度方向与斜面的夹角等于θ
【答案】B,D
【解析】解：设斜面的倾角为θ．
AB、小球落在斜面上，有：tanθ= 
解得：t= 
在竖直方向上的分位移为：y= 
则知当初速度变为原来的 
倍时，竖直方向上的位移变为原来的2倍，所以小球一定落在斜面上的c点，故A错误，B正确；
C、设小球落在斜面上速度与水平方向的夹角为β，则tanβ= 
=2tanθ，即tanβ=2tanθ，所以β一定，则知落在斜面时的速度方向与斜面夹角一定相同．故C错误，D正确．
故选：BD
小球落在斜面上，竖直方向上的位移与水平方向位移的比值一定，运动的时间与初速度有关，根据竖直方向上的位移公式，可得出竖直位移与初速度的关系，从而知道小球的落点．根据速度方向与水平方向的夹角变化，去判断小球两次落在斜面上的速度与斜面的夹角的关系．
练习册系列答案
相关题目
