题目内容
 (2005?长宁区模拟)如图所示,一带电粒子以速度v0沿上板边缘垂直于电场线射入匀强电场,它刚好贴着下板边缘飞出.已知匀强电场两极板长为l,间距为d,求:
(2005?长宁区模拟)如图所示,一带电粒子以速度v0沿上板边缘垂直于电场线射入匀强电场,它刚好贴着下板边缘飞出.已知匀强电场两极板长为l,间距为d,求:(1)如果带电粒子的速度变为2v0,则离开电场时,沿场强方向偏转的距离y为多少?
(2)如果带电粒子的速度变为2v0,板长l不变,当它的竖直位移仍为d时,它的水平位移x为多少?(粒子的重力忽略不计)
分析:(1)带电粒子垂直于电场线射入匀强电场,做类平抛运动,运用运动的分解法分析:带电粒子在水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,根据牛顿第二定律和运动学公式得出加速度a与板间距离d、初速度v0t 板长的关系式,再得到带电粒子的速度变为2v0,沿场强方向偏转的距离y与板间距离d、初速度v0t 板长的关系式.求出y.
(2)当带电粒子的速度变为2v0,板长l不变,当它的竖直位移仍为d时,用同样的方法得到水平位移x与板间距离d、初速度v0t 板长的关系式,运用比例法求出x.
(2)当带电粒子的速度变为2v0,板长l不变,当它的竖直位移仍为d时,用同样的方法得到水平位移x与板间距离d、初速度v0t 板长的关系式,运用比例法求出x.
解答: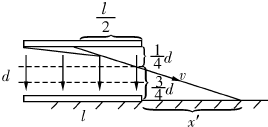 解:因为带电粒子在电场中做类平抛运动,受到的电场力与速度无关,所以a是一定的,则有
解:因为带电粒子在电场中做类平抛运动,受到的电场力与速度无关,所以a是一定的,则有
l=v0t
d=
at 2
得到a=
(1)由题,l=2v0t′
y=
at′2=
?
?(
)2=
(2)如图所示:将速度反向延长交上板的中点,由三角形相似得
=
,得到x′=1.5l
所以水平位移x=l+x′=2.5l
答:
(1)如果带电粒子的速度变为2v0,离开电场时,沿场强方向偏转的距离y=
.
(2)如果带电粒子的速度变为2v0,板长l不变,当它的竖直位移仍为d时,它的水平位移x为2.5l.
 解:因为带电粒子在电场中做类平抛运动,受到的电场力与速度无关,所以a是一定的,则有
解:因为带电粒子在电场中做类平抛运动,受到的电场力与速度无关,所以a是一定的,则有l=v0t
d=
| 1 |
| 2 |
得到a=
2d
| ||
| l2 |
(1)由题,l=2v0t′
y=
| 1 |
| 2 |
| 1 |
| 2 |
2d
| ||
| l2 |
| l |
| 2v0 |
| d |
| 4 |
(2)如图所示:将速度反向延长交上板的中点,由三角形相似得
| x′ | ||
|
| ||
|
所以水平位移x=l+x′=2.5l
答:
(1)如果带电粒子的速度变为2v0,离开电场时,沿场强方向偏转的距离y=
| d |
| 4 |
(2)如果带电粒子的速度变为2v0,板长l不变,当它的竖直位移仍为d时,它的水平位移x为2.5l.
点评:本题中带电粒子垂直进入匀强电场做类平抛运动,采用运动的分解研究,运用比例法是常用的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2005?长宁区模拟)如图所示,两端开口的细长玻璃管的上方有一段水银柱,下端插入水银槽中,若大气压强及气温保持不变,把管子缓慢地竖直向上提起,在管子下端未离开槽中水银面前,图中h的高度变化情况是( )
(2005?长宁区模拟)如图所示,两端开口的细长玻璃管的上方有一段水银柱,下端插入水银槽中,若大气压强及气温保持不变,把管子缓慢地竖直向上提起,在管子下端未离开槽中水银面前,图中h的高度变化情况是( ) (2005?长宁区模拟)如图A、B是两个横截面积不同的竖直圆筒,其中各有一个活塞,它们距离筒底的高度均为h0=0.2m,质量分别为m1=1kg,m2=2kg,活塞下面盛有温度相同且不变的同种气体,活塞上面为真空,两个圆筒的底部是由细管相连通的.如果在A活塞上面再加放一个质量为m=0.5kg的物体,稳定后两活塞的高度差为
(2005?长宁区模拟)如图A、B是两个横截面积不同的竖直圆筒,其中各有一个活塞,它们距离筒底的高度均为h0=0.2m,质量分别为m1=1kg,m2=2kg,活塞下面盛有温度相同且不变的同种气体,活塞上面为真空,两个圆筒的底部是由细管相连通的.如果在A活塞上面再加放一个质量为m=0.5kg的物体,稳定后两活塞的高度差为 (2005?长宁区模拟)如图所示,传送带与水平方向成θ=30°角,皮带的AB部分长为L=3.25m,皮带以速度v=2m/s顺时针方向运动,在A端无初速地放上一质量为m=1kg的小物体,小物体与皮带间的动摩擦因数为μ=
(2005?长宁区模拟)如图所示,传送带与水平方向成θ=30°角,皮带的AB部分长为L=3.25m,皮带以速度v=2m/s顺时针方向运动,在A端无初速地放上一质量为m=1kg的小物体,小物体与皮带间的动摩擦因数为μ=