题目内容
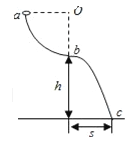
【题目】如图,位于竖直平面内的光滑轨道由四分之一圆弧ab和抛物线bc组成,圆弧半径Oa水平,b点为抛物线顶点.已知h=2m,s=![]() m.取重力加速度大小g=10m/s2.
m.取重力加速度大小g=10m/s2.
(1)一小环套在轨道上从a点由静止滑下,当其在bc段轨道运动时,与轨道之间无相互作用力,求圆弧轨道的半径;
(2)若环从b点由静止因微小扰动而开始滑下,求环到达c点时速度的水平分量的大小.
【答案】(1)0.25m;(2)![]()
【解析】 (1)小环套在bc段轨道运动时,与轨道之间无相互作用力,则说明下落到b点时的速度使得小环套做平抛运动的轨迹与轨道bc重合,
故有![]() ,
, ![]()
从ab滑落过程中,根据动能定理可得
![]()
联立三式可得![]() 。
。
(2)下滑过程中,初速度为零,只有重力做功,根据动能定理可得![]()
因为物体滑到c点时与竖直方向的夹角等于(1)问中做平抛运动过程中经过c点时速度与竖直方向的夹角相等,设为![]() ,则根据平抛运动规律可知:
,则根据平抛运动规律可知: 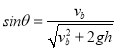
根据运动的合成与分解可得: ![]()
联立可得: ![]() 。
。

练习册系列答案
相关题目