题目内容
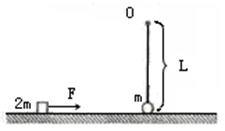
(18分)如图所示,长为L的不可伸长的绳子一端固定在O点,另一端系质量为m的小球,小球静止在光滑水平面上。现用大小为F水平恒力作用在另一质量为2m的物块上,使其从静止开始向右运动,一段时间后撤去该力,物块与小球发生正碰后速度大小变为原来的一半而速度方向不变,小球恰好能在竖直平面内做圆周运动。已知重力加速度为g,小球和物体均可视为质点,试求:
(1)小物块碰撞前速度V0的大小;
(2)碰撞过程中系统损失的机械能;
(3)恒力F作用时间。

(1)小物块碰撞前速度V0的大小;
(2)碰撞过程中系统损失的机械能;
(3)恒力F作用时间。
(1)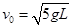 (2)
(2)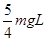 (3)
(3)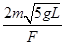
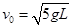 (2)
(2)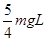 (3)
(3)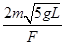
试题分析:(1) 小球恰好能在竖直平面内做圆周运动,即通过最高点对轨道压力为0,此时设最高点速度为V,有
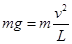 ,得出
,得出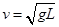 ,
, 小球从最低点摆到最高点过程,根据动能定理有
 解得小球最低点即碰后的速度
解得小球最低点即碰后的速度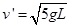
小物块和小球碰撞过程中,动量守恒定律 有

解得
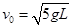
(2)二者碰撞前的系统总动能为
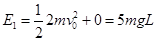
碰撞后的动能为
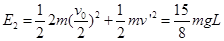
碰撞前后只有动能发生了变化,因此损失的机械能

(3)物块在光滑的水平桌面上,有拉力F作用时做匀加速运动,加速度
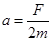
力F撤去后在光滑的水平面做匀速运动,设加速时间为t则有
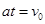
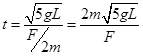

练习册系列答案
相关题目
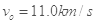 的速度时进入地月转移轨道向月球飞去。后6次点火的主要作用是修正飞行方向和被月球捕获时的紧急刹车,最终把卫星送入离月面h=200km高的工作轨道(可视为匀速圆周运动)。已知地球质量是月球质量的81倍,
的速度时进入地月转移轨道向月球飞去。后6次点火的主要作用是修正飞行方向和被月球捕获时的紧急刹车,最终把卫星送入离月面h=200km高的工作轨道(可视为匀速圆周运动)。已知地球质量是月球质量的81倍,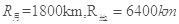 ,卫星质量为2350kg,地球表面重力加速度
,卫星质量为2350kg,地球表面重力加速度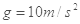 ,引力恒量
,引力恒量 。(结果保留一位有效数字)求:
。(结果保留一位有效数字)求:
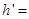 2.5m,求小球在半圆轨道上克服摩擦力所做的功.
2.5m,求小球在半圆轨道上克服摩擦力所做的功.
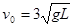 向右匀速行驶。突然,小车因撞到正前方固定障碍物,速度立即变为零,小球以v0为初速度开始在竖直平面内做圆周运动。当小球第一次到达最高点时,地面对车的支持力恰好为零。已知在此过程中,小车一直未动,重力加速度为g。求:
向右匀速行驶。突然,小车因撞到正前方固定障碍物,速度立即变为零,小球以v0为初速度开始在竖直平面内做圆周运动。当小球第一次到达最高点时,地面对车的支持力恰好为零。已知在此过程中,小车一直未动,重力加速度为g。求: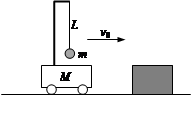
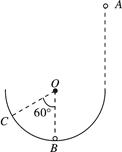
 的小球以某一速度从C点运动到A点进入轨道,小球与水平地面间的动摩擦因数为
的小球以某一速度从C点运动到A点进入轨道,小球与水平地面间的动摩擦因数为 。它经过最高点B飞出后又能落回到C点,AC=2R。求小球从C点开始运动时的初速度v0的大小。
。它经过最高点B飞出后又能落回到C点,AC=2R。求小球从C点开始运动时的初速度v0的大小。



