题目内容
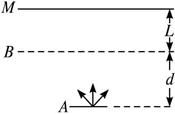
如图所示，在厚铅板A的右表面P处放一个β放射源（β放射源是一个发射出高速电子的源），放出的电子速度均为v0，方向沿四面八方，且机会相等．在B处放一块平行于A的足够大的金属网，A、B间加一场强为E、方向水平向左的匀强电场，A、B间相距d，在B的右侧距金属网L处放置一荧光屏M，以观察到达荧光屏的电子，（设电子的电荷量为e，质量为m）．求（1）电子到达金属网的最长时间；
（2）荧光屏上出现亮点范围的面积．
分析：（1）平行于A板的电子最后到达B，运动时间最长，此类电子做类平抛运动，由平抛运动知识可求运动时间
（2）电子透过金属网将作匀速直线运动，由几何关系解得电子到达的最远处，由于电子放射方向沿四面八方，且机会相等，故发光面积应为圆形，由圆的面积公式求得答案
（2）电子透过金属网将作匀速直线运动，由几何关系解得电子到达的最远处，由于电子放射方向沿四面八方，且机会相等，故发光面积应为圆形，由圆的面积公式求得答案
解答：解：（1）电子在电场中做匀加速运动，加速度大小为：
a=
①
平行于A板的电子将做类平抛运动，最迟到达金属网，设时间为t，由运动学公式得：
d=
at2②
由①②得，t=
③
（2）平行于A板的电子到达金属网时，垂直于电场方向的位移为：
s1=v0t④
电子透过金属网后将改为匀速直线运动，其中沿垂直于金属网方向的分速度为：
v1=at⑤
电子透过金属网达到光屏经过的时间：
t2=
⑥
此时间内电子沿平行于金属板方向的位移为：
s2=v0t2⑦
由题意知，光屏上发光区域的半径为：
r=s1+s2⑧
发光区域面积为：S=πr2⑨
由①③～⑨得：S=πv02（
+2L+
）
答：（1）电子到达金属网的最长时间为
（2）发光区域面积为πv02（
+2L+
）
a=
| Ee |
| m |
平行于A板的电子将做类平抛运动，最迟到达金属网，设时间为t，由运动学公式得：
d=
| 1 |
| 2 |
由①②得，t=
|
（2）平行于A板的电子到达金属网时，垂直于电场方向的位移为：
s1=v0t④
电子透过金属网后将改为匀速直线运动，其中沿垂直于金属网方向的分速度为：
v1=at⑤
电子透过金属网达到光屏经过的时间：
t2=
| L |
| v1 |
此时间内电子沿平行于金属板方向的位移为：
s2=v0t2⑦
由题意知，光屏上发光区域的半径为：
r=s1+s2⑧
发光区域面积为：S=πr2⑨
由①③～⑨得：S=πv02（
| 2dm |
| Ee |
| EeL2 |
| 2dm |
答：（1）电子到达金属网的最长时间为
|
（2）发光区域面积为πv02（
| 2dm |
| Ee |
| EeL2 |
| 2dm |
点评：电子的类平抛运动经常考察，要求学生能熟练的应用运动的分解的观点加以推导和分析，电子射出电场后的运动也应利用分解的观点解决，其中的运算量稍大一些
练习册系列答案
阅读快车系列答案
相关题目
（2006?上海模拟）如图所示，在厚铅板A表面上放有一放射源M，它向各个方向射出相同速率的质量为m、电量为q的β粒子（重力可忽略不计）．为了测出β粒子的射出速率，在金属网B与A板之间加电压U（A板电势低），发现荧光屏C上有半径为R的圆形亮斑，知道A、B间的距离为d，B、C间距离为L．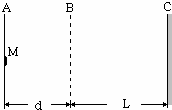
如图所示，在厚铅板A表面上放有一放射源M，它可向各个方向射出相同速率的质量为m、电量为q的β粒子（重力可忽略不计）．为了测出β粒子从放射源M射出的速率，可在金属网B与A板之间加电压U（A板电势低），使β粒子经A板与金属网B之间的匀强电场加速后穿过金属网B撞到荧光屏C上发出荧光，现发现荧光屏C上有半径为R的圆形亮斑，知道A、B间的距离为d，和B、C间距离为L．
