题目内容
15.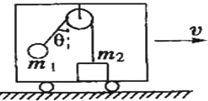 车厢顶部固定一滑轮,在跨过定滑轮绳子的两端各系一个物体,质量分别为m1、m2,且m2>m1,m2静止在车厢底板上,当车厢向右运动时,m1、m2与车厢保持相对静止,系m1的那段绳子与竖直方向夹角为θ,如图所示,绳子的质量、滑轮与绳子的摩擦忽略不计,下列说法不正确的是( )
车厢顶部固定一滑轮,在跨过定滑轮绳子的两端各系一个物体,质量分别为m1、m2,且m2>m1,m2静止在车厢底板上,当车厢向右运动时,m1、m2与车厢保持相对静止,系m1的那段绳子与竖直方向夹角为θ,如图所示,绳子的质量、滑轮与绳子的摩擦忽略不计,下列说法不正确的是( )| A. | 车厢的加速度为gtanθ | B. | 车厢底板对m2的支持力为(m1+m2)g | ||
| C. | 绳子中的张力大小为m1gcosθ | D. | 车厢底板对m2的摩擦力为m2gtanθ |
分析 先对m1受力分析,求出绳子的张力大小,根据合力由牛顿第二定律求出车厢的加速度.再对m2受力分析,可以得出车厢底板对m2的支持力,以及摩擦力.
解答 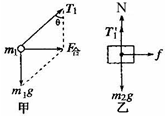 解:对物体m1受力分析如图甲所示,
解:对物体m1受力分析如图甲所示,
竖直方向:T1cosθ=m1g;;;①
水平方向:T1sinθ=m1a
解得a=gtanθ,车厢与m1的加速度相同为gtanθ,方向水平向右,故A正确.
解得T1=m1gcosθ,即绳子的张力大小为m1gcosθ,故C正确.
对物体m2受力分析如图乙所示.
竖直方向:T1+N=m2g
水平方向:f=m2a
解得:N=m2g−m1gcosθ,f=m2gtanθ.
故B错误,故D正确.
本题选说法不正确的,故选:B.
点评 题目关键在于分别对两个物体进行受力分析,综合考查了力的合成,牛顿第二定律,综合性较强.

练习册系列答案
相关题目
6.一个质点做直线运动,初速度的大小为2m/s,末速度的大小为8m/s,则( )
| A. | 速度改变量的大小一定是10m/s | |
| B. | 速度改变量的大小可能是6m/s | |
| C. | 速度改变量的方向一定与初速度方向相同 | |
| D. | 速度改变量的方向可能与初速度方向相反 |
3.下面有关说法中正确是( )
| A. | 物体对水平桌面的压力就是重力 | |
| B. | 重力的方向可能指向地心 | |
| C. | 杆的弹力一定沿杆方向 | |
| D. | 物体对桌面的压力是桌面发生形变产生的 |
10.物体由静止开始做加速度大小为a1的匀加速直线运动,当速度达到v时,改为加速度大小为a2的匀减速直线运动,直至速度为零.在匀加速和匀减速运动过程中物体的位移大小和所用时间分别为x1、x2和t1、t2,下列各式不成立的是( )
| A. | x1x2=t1t2 | B. | v=2(x1+x2)t1+t2 | ||
| C. | x1t1=x2t2=x1+x2t1+t2 | D. | a1a2=t1t2 |
20.19世纪20年代,以塞贝克(数学家)为代表的科学家已认识到:温度差会引起电流.安培考虑到地球自转造成了太阳照射后正面与背面的温度差,从而提出如下假设:地球磁场是由地球的环形电流引起的,则该假设中的电流方向是( )
| A. | 由西向东 | B. | 由赤道向两极 | C. | 由南向北 | D. | 由东向西 |
7.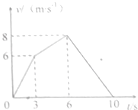 物体沿竖直方向运动的v-t图象如图所示(取竖直向上为正方向),由图象可以看出物体( )
物体沿竖直方向运动的v-t图象如图所示(取竖直向上为正方向),由图象可以看出物体( )
 物体沿竖直方向运动的v-t图象如图所示(取竖直向上为正方向),由图象可以看出物体( )
物体沿竖直方向运动的v-t图象如图所示(取竖直向上为正方向),由图象可以看出物体( )| A. | 0~10s内一直向上运动 | B. | 3~6s内加速度最大 | ||
| C. | 0~3s内向上运动,6~10s内向下运动 | D. | 0~3s和6~10s内加速度方向不变 |
4.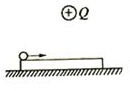 如图所示,在水平放置的光滑接地金属板中点的正上方,有带正电的点电荷Q,一表面绝缘带正电的金属球(可视为质点,且不影响原电场)自左以速度v0开始在金属板上向右运动,在运动过程中( )
如图所示,在水平放置的光滑接地金属板中点的正上方,有带正电的点电荷Q,一表面绝缘带正电的金属球(可视为质点,且不影响原电场)自左以速度v0开始在金属板上向右运动,在运动过程中( )
 如图所示,在水平放置的光滑接地金属板中点的正上方,有带正电的点电荷Q,一表面绝缘带正电的金属球(可视为质点,且不影响原电场)自左以速度v0开始在金属板上向右运动,在运动过程中( )
如图所示,在水平放置的光滑接地金属板中点的正上方,有带正电的点电荷Q,一表面绝缘带正电的金属球(可视为质点,且不影响原电场)自左以速度v0开始在金属板上向右运动,在运动过程中( )| A. | 小球做先减速后加速运动 | B. | 小球做匀速直线运动 | ||
| C. | 点电荷Q对小球为库仑力不做功 | D. | 电场力对小球先做正功后做负功 |