题目内容
如图所示,有一垂直于纸面向外的有界匀强磁场,磁场的磁感应强度为B,其边界为一等腰直角三角形(边界上有磁场),ACD为三角形的三个顶点,AC=AD=L.今有一质量为m、电荷量为+q的粒子(不计重力),以速度v= 从CD边上的某点P既垂直于CD边又垂直于磁场的方向射入,然后从AD边上某点Q射出,则有( )
从CD边上的某点P既垂直于CD边又垂直于磁场的方向射入,然后从AD边上某点Q射出,则有( )
A.DP< L L | B.DP< L L | C.DQ≤ L L | D.DQ≤ L L |
解析试题分析:粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,临界轨迹是恰好与AC边相切,然后结合几何关系分析即可.
解:A、B、粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,轨道半径为:
r= =
=
临界轨迹圆恰好与AC边相切,如图所示:
结合几何关系,有:
DP=CD﹣CP=CD﹣(CO﹣OP)= ﹣(
﹣( r﹣r)=
r﹣r)= L
L
故DP小于 L,粒子可以从AD边射出;故A正确,B错误;
L,粒子可以从AD边射出;故A正确,B错误;
C、D、结合几何关系,根据勾股定理,有:
EO2+QE2=QO2
即(r﹣AQ)2+QE2=r2
(r﹣AQ)2+(L﹣r)2=r2
解得:AQ=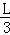 ,故QD=
,故QD=
故粒子可以从AD边离D的 点射出,故C正确,D错误;
点射出,故C正确,D错误;
故选:AC.
点评:本题关键是先结合洛伦兹力提供向心力列式求解出轨道半径,然后画出临界轨迹,最后结合几何关系列式求解.

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案如图所示,水平直导线中通有恒定电流I,导线的正上方处有一电子初速度v0,其方向与电流方向相同,以后电子将( )
| A.沿路径a运动,曲率半径变小 | B.沿路径a运动,曲率半径变大 |
| C.沿路径b运动,曲率半径变小 | D.沿路径b运动,曲率半径变大 |
如图为某磁谱仪部分构件的示意图。图中,永磁铁提供匀强磁场,硅微条径迹探测器可以探测粒子在其中运动的轨迹。宇宙射线中有大量的电子、正电子和质子。当这些粒子从上部垂直进入磁场时,下列说法正确的是
| A.电子与正电子的偏转方向一定不同 |
| B.电子和正电子在磁场中的运动轨迹一定相同 |
| C.仅依据粒子的运动轨迹无法判断此粒子是质子还是正电子 |
| D.粒子的动能越大,它在磁场中运动轨迹的半径越小 |
如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L)。一质量为m、电荷量为e的电子从a点以初速度v0平行于x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度的方向与x轴正方向的夹角为60°.下列说法正确的是
A.电子在磁场中运动的时间为 |
B.电子在磁场中运动的时间为 |
C.磁场区域的圆心坐标为( , , ) ) |
| D.电子在磁场中做圆周运动的圆心坐标为(0,-2L) |
两根足够长的光滑导轨竖直放置,间距为L,底端接阻值为R的电阻。将质量为m的金属棒悬挂在一个固定的轻弹簧下端,金属棒和导轨接触良好,导轨所在平面与磁感应强度为B的匀强磁场垂直,如图所示。除电阻R外其余电阻不计。现将金属棒从弹簧原长位置由静止释放。则
| A.释放瞬间金属棒的加速度小于重力加速度g |
| B.金属棒向下运动时,流过电阻R的电流方向为b→a |
C.金属棒的速度为v时,所受的安培力大小为 |
| D.电阻R上产生的总热量等于金属棒重力势能的减少 |
如图所示的螺线管正上方放置一小磁针,当闭合开关S后,小磁针的指向如图所示,其中黑色的那一端为小磁针的N极,下列判断正确的是 
| A.电源左端为正、右端为负,线圈左端为N极,右端为S极 |
| B.电源左端为负、右端为正,线圈左端为N极,右端为S极 |
| C.电源左端为负、右端为正,线圈左端为S极,右端为N极 |
| D.电源左端为正、右端为负,线圈左端为S极,右端为N极 |
回旋加速器是用来加速带电粒子的装置,如图所示.它的核心部分是两个D形金属盒,两盒相距很近,分别和高频交流电源相连接,两盒间的窄缝中形成匀强电场,使带电粒子每次通过窄缝都得到加速.两盒放在匀强磁场中,磁场方向垂直于盒底面,带电粒子在磁场中做圆周运动,通过两盒间的窄缝时反复被加速,直到达到最大圆周半径时通过特殊装置被引出.如果用同一回旋加速器分别加速氚核( )和α粒子(
)和α粒子( )比较它们所加的高频交流电源的周期和获得的最大动能的大小,有
)比较它们所加的高频交流电源的周期和获得的最大动能的大小,有
| A.加速氚核的交流电源的周期较大,氚核获得的最大动能也较大 |
| B.加速氚核的交流电源的周期较大,氚核获得的最大动能较小 |
| C.加速氚核的交流电源的周期较小,氚核获得的最大动能也较小 |
| D.加速氚核的交流电源的周期较小,氚核获得的最大动能较大 |
如图所示,条形磁铁放在光滑的斜面上(斜面固定不动)。用平行于斜面的轻弹簧拉住而平衡,A为水平放置的直导线的截面,导线中无电流时,磁铁对斜面的压力为F1;导线中有电流时,磁铁对斜面的压力为F2,此时弹簧的伸长量减小,则( )
| A.F1<F2,A中电流方向向内 |
| B.F1<F2,4中电流方向向外 |
| C.F1>F2,A中电流方向向内 |
| D.F1>F2,A中电流方向向外 |
