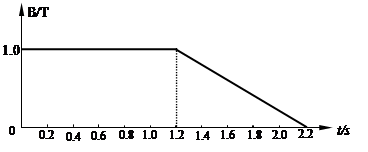题目内容
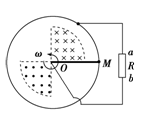
(20分)如图(甲)所示,两光滑导轨都由水平、倾斜两部分圆滑对接而成,相互平行放置,两导轨相距L=lm ,倾斜导轨与水平面成θ=30°角,倾斜导轨的下面部分处在一垂直斜面的匀强磁场区I中,I区中磁场的磁感应强度B1随时间变化的规律如图(乙)所示,图中t1、t2未知。水平导轨足够长,其左端接有理想电流表G和定值电阻R=3Ω,水平导轨处在一竖直向上的匀强磁场区Ⅱ中,Ⅱ区中的磁场恒定不变,磁感应强度大小为B2=1T ,在t=0时刻,从斜轨上磁场I 区外某处垂直于导轨水平释放一金属棒ab,棒的质量m=0.1kg,电阻r=2Ω,棒下滑时与导轨保持良好接触,棒由倾斜导轨滑向水平导轨时无机械能损失,导轨的电阻不计。若棒在斜面上向下滑动的整个过程中,电流表G的示数大小保持不变,t2时刻进入水平轨道,立刻对棒施一平行于框架平面沿水平方向且与杆垂直的外力。(g取10m/s2)求:

(l)ab 棒进入磁场区I 时的速度v;
(2)磁场区I在沿斜轨方向上的宽度d;
(3)棒从开始运动到刚好进入水平轨道这段时间内ab棒上产生的热量;
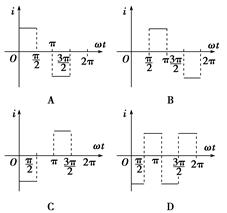
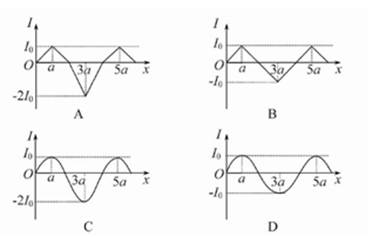
(4)若棒在t2时刻进入水平导轨后,电流表G的电流大小I随时间t变化的关系如图(丙)所示(I0未知),已知t2到t3的时间为0.5s,t3到t4的时间为1s,请在图(丁)中作出t2到t4时间内外力大小
F随时间t变化的函数图像。

(l)ab 棒进入磁场区I 时的速度v;
(2)磁场区I在沿斜轨方向上的宽度d;
(3)棒从开始运动到刚好进入水平轨道这段时间内ab棒上产生的热量;
(4)若棒在t2时刻进入水平导轨后,电流表G的电流大小I随时间t变化的关系如图(丙)所示(I0未知),已知t2到t3的时间为0.5s,t3到t4的时间为1s,请在图(丁)中作出t2到t4时间内外力大小
F随时间t变化的函数图像。
(1)2.5m/s(2)0.625m(3)0.375J(4)见解析
(20分)
(1)电流表的示数不变,说明在整个下滑过程中回路的的电动势是不变的,说明在B变化时和不变时感应电动势大小一样,所以可以判断在t1时刻棒刚好进入磁场区域且做匀速直线运动。
mgsin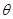 -BIL=0,
-BIL=0, 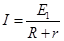 , E1=BLV, 代入数值得v=2.5m/s (4分)
, E1=BLV, 代入数值得v=2.5m/s (4分)
(2)没进入磁场以前做匀加速直线运动,加速度是 a=gsin300=5m/s2, v=at, t1=0.5s ,
下滑的距离是s1=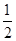 at2=0.625m,再没进入磁场以前,由于B均匀变化,所以E2=
at2=0.625m,再没进入磁场以前,由于B均匀变化,所以E2= ,
,
又E1=BLV E1= E2 , 4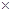 1
1 d=1
d=1 1
1 2.5, d=0.625m (6分)
2.5, d=0.625m (6分)
(3)ab棒进入磁场以前,棒上产生的热量为 Q1=I2Rt1=0.52×2×0.5J=0.25J
取ab棒在斜轨磁场中运动为研究过程, mgd sin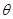 -Q2=0 Q2="0.3125J."
-Q2=0 Q2="0.3125J."
此时,棒上产生的热量是Q2r=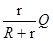 =0.125J
=0.125J
则棒上产生的总热量是Qr= Q1+Q2r="0.375" J (6分)
或:Qr=I2R(t1+t2)=0.52×2×(0.5+0.25)J=0.375J
(4) 因为E=BLv,所以刚进水平轨道时时的电动势是E=2.5V, I0=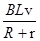 =0.5A
=0.5A
取t2时刻为零时刻,则根据图线可以写出I-t的方程式:I=0.5-tˊ,I=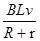 ,
,
则v="2.5-5" tˊ,所以a1=5m/s2.有牛顿第二定律可得:F+BIL=ma1,F+I=1 F=tˊ
画在坐标系里。

由丙图可以同理得出棒运动的加速度大小是a2=2.5m/s2,依据牛顿定律得F-BIL=ma2
取t3时刻为零时刻,可以写出t3时刻后的I与时间的关系式,I="0.5" t ,代入上面的式子可以得到F=0.25+0.5t画在坐标系里。(图中图线作为参考) (4分)
本题考查的是电磁感应定律和力学综合的相关问题,根据电磁感应定律和匀速直线运动的受力平衡可以求出运动速度;根据匀加速直线运动的规律求出磁场宽度;根据焦耳定律和功能关系可以求出产生的焦耳热;根据欧姆定律和牛顿第二定律可以得出力与时间的关系;
(1)电流表的示数不变,说明在整个下滑过程中回路的的电动势是不变的,说明在B变化时和不变时感应电动势大小一样,所以可以判断在t1时刻棒刚好进入磁场区域且做匀速直线运动。
mgsin
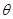 -BIL=0,
-BIL=0, 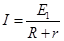 , E1=BLV, 代入数值得v=2.5m/s (4分)
, E1=BLV, 代入数值得v=2.5m/s (4分)(2)没进入磁场以前做匀加速直线运动,加速度是 a=gsin300=5m/s2, v=at, t1=0.5s ,
下滑的距离是s1=
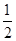 at2=0.625m,再没进入磁场以前,由于B均匀变化,所以E2=
at2=0.625m,再没进入磁场以前,由于B均匀变化,所以E2= ,
, 又E1=BLV E1= E2 , 4
 1
1 d=1
d=1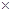 1
1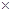 2.5, d=0.625m (6分)
2.5, d=0.625m (6分)(3)ab棒进入磁场以前,棒上产生的热量为 Q1=I2Rt1=0.52×2×0.5J=0.25J
取ab棒在斜轨磁场中运动为研究过程, mgd sin
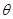 -Q2=0 Q2="0.3125J."
-Q2=0 Q2="0.3125J." 此时,棒上产生的热量是Q2r=
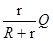 =0.125J
=0.125J 则棒上产生的总热量是Qr= Q1+Q2r="0.375" J (6分)
或:Qr=I2R(t1+t2)=0.52×2×(0.5+0.25)J=0.375J
(4) 因为E=BLv,所以刚进水平轨道时时的电动势是E=2.5V, I0=
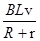 =0.5A
=0.5A取t2时刻为零时刻,则根据图线可以写出I-t的方程式:I=0.5-tˊ,I=
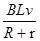 ,
,则v="2.5-5" tˊ,所以a1=5m/s2.有牛顿第二定律可得:F+BIL=ma1,F+I=1 F=tˊ
画在坐标系里。

由丙图可以同理得出棒运动的加速度大小是a2=2.5m/s2,依据牛顿定律得F-BIL=ma2
取t3时刻为零时刻,可以写出t3时刻后的I与时间的关系式,I="0.5" t ,代入上面的式子可以得到F=0.25+0.5t画在坐标系里。(图中图线作为参考) (4分)
本题考查的是电磁感应定律和力学综合的相关问题,根据电磁感应定律和匀速直线运动的受力平衡可以求出运动速度;根据匀加速直线运动的规律求出磁场宽度;根据焦耳定律和功能关系可以求出产生的焦耳热;根据欧姆定律和牛顿第二定律可以得出力与时间的关系;

练习册系列答案
相关题目
 L2),以如图所示位置为计时起点。求:
L2),以如图所示位置为计时起点。求:
 的时间内,通过小灯泡的电荷量;
的时间内,通过小灯泡的电荷量;

 πr2Bωsinωt
πr2Bωsinωt rBv
rBv
 .
.