Question

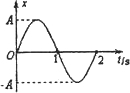重庆市某中学生在本校实验室利用一单摆做小角度摆动，通过实验得到摆球振动位移x随时间t变化的关系如题图所示，则下列说法正确的是 （　　）

A、t=0时刻摆球加速度为零，所受合外力为零

B、t=0时刻与t=ls时刻摆球的速度相同

C、该同学所用单摆摆长约为1m

D、t=0.5s时刻摆线的张力最大

Answer 1

分析：根据位移时间关系图象得到周期，根据单摆的周期公式得到摆长；将重力沿着半径方向和切线方向进行正交分解，沿半径方向的合力提供向心力，重力的切线分量提供回复力．

解答：解：A、t=0时刻，位移为零，单摆经过平衡位置，回复力为零，但拉力和重力的合力提供向心力，故合力不为零，加速度也不为零，为零的是回复力产生的切线加速度，故A错误；
B、t=0时刻与t=ls时刻摆球的位移都为零，但速度方向相反，故B错误；
C、从图象得到单摆的周期为2s，根据周期公式T=2π

L g

，可以解得摆长L=1m，故C正确；
D、细线拉力和重力的沿半径方向的分力的合力提供向心力，t=0.5s时刻，位移最大，速度最小，故拉力最小，故D错误；
故选C．

点评：本题关键要知道单摆的回复力的来源和向心力的来源，然后根据图象得到周期，根据周期公式求解摆长．