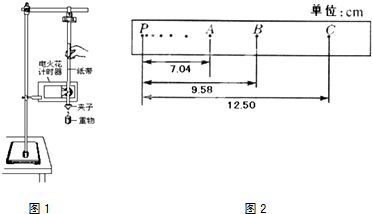
题目内容
3.质量为1Kg的小球从高20m处自由落到软垫上,反弹后最大高度为5.0m,小球与软垫接触的时间为1.0s,在接触时间内受到软垫弹力的冲量大小是多少?分析 由自由落体运动规律及竖直上抛规律可求得接触软垫前后的速度,再由动量定理可求得冲量的大小.
解答 解:在接地过程中应用动量定理,设向上为正方向;则有:
IN-mgt=mv2-mv1
又因为下落时是自由落体运动,有:${v_1}^2=2g{h_1}$
代入数据解得:v1=20m/s
而上升过程为竖直上抛运动,有:${h_2}=\frac{{{v_2}^2}}{2g}$
代入数据解得:v2=10m/s
$\begin{array}{l}{I_N}=m{v_2}-m{v_1}+mgt=1×10-1×(-20)+1×10×1\\ \;\;\;\;\;=40N•s\end{array}$
答:接触时间内受到软垫弹力的冲量大小为40N•s.
点评 本题考查动量定理的应用,要注意动量、冲量均为矢量;在解题时要注意方向性.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
13.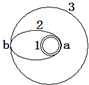 如图所示,是某次发射人造卫星的示意图,人造卫星先在半径为r的近地圆周轨道1上运动,然后改在椭圆轨道2上运动,最后在半径为7r的圆周轨道3上运动,a点是轨道1、2的交点,b点是轨道2、3的交点,人造卫星在轨道1上a点的速度为v1a,在轨道2上a点的速度为v2a,在轨道2上b点的速度为v2b,在轨道3上b点的速度为v3b,已知卫星在圆轨道运行时的引力势能为Ep=-$\frac{GMm}{r}$选择无穷远处为势能零点,r是卫星与中心天体的球心距,下列说法正确的是( )
如图所示,是某次发射人造卫星的示意图,人造卫星先在半径为r的近地圆周轨道1上运动,然后改在椭圆轨道2上运动,最后在半径为7r的圆周轨道3上运动,a点是轨道1、2的交点,b点是轨道2、3的交点,人造卫星在轨道1上a点的速度为v1a,在轨道2上a点的速度为v2a,在轨道2上b点的速度为v2b,在轨道3上b点的速度为v3b,已知卫星在圆轨道运行时的引力势能为Ep=-$\frac{GMm}{r}$选择无穷远处为势能零点,r是卫星与中心天体的球心距,下列说法正确的是( )
 如图所示,是某次发射人造卫星的示意图,人造卫星先在半径为r的近地圆周轨道1上运动,然后改在椭圆轨道2上运动,最后在半径为7r的圆周轨道3上运动,a点是轨道1、2的交点,b点是轨道2、3的交点,人造卫星在轨道1上a点的速度为v1a,在轨道2上a点的速度为v2a,在轨道2上b点的速度为v2b,在轨道3上b点的速度为v3b,已知卫星在圆轨道运行时的引力势能为Ep=-$\frac{GMm}{r}$选择无穷远处为势能零点,r是卫星与中心天体的球心距,下列说法正确的是( )
如图所示,是某次发射人造卫星的示意图,人造卫星先在半径为r的近地圆周轨道1上运动,然后改在椭圆轨道2上运动,最后在半径为7r的圆周轨道3上运动,a点是轨道1、2的交点,b点是轨道2、3的交点,人造卫星在轨道1上a点的速度为v1a,在轨道2上a点的速度为v2a,在轨道2上b点的速度为v2b,在轨道3上b点的速度为v3b,已知卫星在圆轨道运行时的引力势能为Ep=-$\frac{GMm}{r}$选择无穷远处为势能零点,r是卫星与中心天体的球心距,下列说法正确的是( )| A. | 轨道1、2、3的周期之比为7$\sqrt{7}$:8:1 | |
| B. | v2a>v1a>v2b>v3b | |
| C. | v2a>v1a>v3b>v2b | |
| D. | 圆周轨道1和3上运行时,卫星和地球系统的机械能之比为1:14 |
8.下列说法中正确的是( )
| A. | 只要物体受力的同时又有位移发生,则一定有力对物体做功 | |
| B. | 一对作用力和反作用力在相同时间内做的功一定大小相等,正负相反 | |
| C. | 机器做功越多,其功率越大 | |
| D. | 汽车上坡的时候,司机必须换挡,其目的是减小速度,得到较大的牵引力 |
15. 如图所示,两人各用6N的力沿相反方向拉一轻质弹簧的两端.当弹簧静止时,它所受的弹力和合力大小分别是( )
如图所示,两人各用6N的力沿相反方向拉一轻质弹簧的两端.当弹簧静止时,它所受的弹力和合力大小分别是( )
 如图所示,两人各用6N的力沿相反方向拉一轻质弹簧的两端.当弹簧静止时,它所受的弹力和合力大小分别是( )
如图所示,两人各用6N的力沿相反方向拉一轻质弹簧的两端.当弹簧静止时,它所受的弹力和合力大小分别是( )| A. | 6N,0N | B. | 12N,12N | C. | 12N,0N | D. | 6N,6N |
12.关于布朗运动,下列说法中不正确的是( )
| A. | 布朗运动是微观粒子运动,牛顿运动定律不再适用 | |
| B. | 布朗运动是液体分子无规则运动的反映 | |
| C. | 强烈的阳光射入较暗的房间内,在光束中可以看到有悬浮在空气中的微尘不停地做无规则运动,这也是一种布朗运动 | |
| D. | 因为布朗运动的激烈程度跟温度有关,所以布朗运动也叫做热运动 |
13.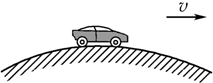 如图所示,汽车以一定的速度经过一个圆弧形桥面的顶点时,关于汽车的受力及汽车对桥面的压力情况,以下说法正确的是( )
如图所示,汽车以一定的速度经过一个圆弧形桥面的顶点时,关于汽车的受力及汽车对桥面的压力情况,以下说法正确的是( )
 如图所示,汽车以一定的速度经过一个圆弧形桥面的顶点时,关于汽车的受力及汽车对桥面的压力情况,以下说法正确的是( )
如图所示,汽车以一定的速度经过一个圆弧形桥面的顶点时,关于汽车的受力及汽车对桥面的压力情况,以下说法正确的是( )| A. | 在竖直方向汽车可能只受两个力:重力和桥面的支持力 | |
| B. | 在竖直方向汽车受到三个力:重力、桥面的支持力和向心力 | |
| C. | 在竖直方向汽车可能只受重力 | |
| D. | 汽车对桥面的压力可能为0 |
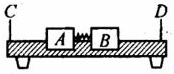 如图所示,气垫导轨是常用的一种实验仪器.它是利用气泵使带孔的导轨与滑块之间形成气垫,使滑块悬浮在导轨上,滑块在导轨上的运动可视为没有摩擦.我们可以用带竖直挡板C、D的气垫导轨以及滑块A、B来验证动量守恒定律,实验装置如图所示(弹簧的长度忽略不计),采用的实验步骤如下:
如图所示,气垫导轨是常用的一种实验仪器.它是利用气泵使带孔的导轨与滑块之间形成气垫,使滑块悬浮在导轨上,滑块在导轨上的运动可视为没有摩擦.我们可以用带竖直挡板C、D的气垫导轨以及滑块A、B来验证动量守恒定律,实验装置如图所示(弹簧的长度忽略不计),采用的实验步骤如下: