题目内容
用水平力F拉一质量为m的物体,由静止开始沿水平面匀加速前进时间t,物体和地面间动摩擦因数为μ,重力加速度为g. 求:
(1)力F对物体做的功;
(2)合外力对物体做的总功.
(1)力F对物体做的功;
(2)合外力对物体做的总功.
分析:(1)利用牛顿第二定律求出加速度,再利用运动学公式求出位移,由W=Fx求出拉力做功;
(2)由W=Fx求出拉力做功;
(2)由W=Fx求出拉力做功;
解答:解:(1)由牛顿第二定律可得
F-μmg=ma
在时间t内通过的位移为
s=
at2
力F做功为
WF=FS
由以上三式可解得:WF=
;
(2)物体受到的合力为
F合=F-μmg
合力做功为
W合=F合S;
解得:W合=
;
答:(1)力F对物体做的功为
;
(2)合外力对物体做的总功为
.
F-μmg=ma
在时间t内通过的位移为
s=
| 1 |
| 2 |
力F做功为
WF=FS
由以上三式可解得:WF=
| F(F-μmg)t2 |
| 2m |
(2)物体受到的合力为
F合=F-μmg
合力做功为
W合=F合S;
解得:W合=
| (F-μmg)t2 |
| 2m |
答:(1)力F对物体做的功为
| F(F-μmg)t2 |
| 2m |
(2)合外力对物体做的总功为
| (F-μmg)t2 |
| 2m |
点评:本题考查了功的计算、牛顿第二定律的应用,明确功的公式即可顺利求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
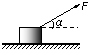 如图所示,用一与水平方向成α的力F拉一质量为m的物体,使它沿水平方向匀速移动距离s,若物体和地面间的动摩擦因数为μ,则此力F对物体做的功,下列表达式中正确的有( )
如图所示,用一与水平方向成α的力F拉一质量为m的物体,使它沿水平方向匀速移动距离s,若物体和地面间的动摩擦因数为μ,则此力F对物体做的功,下列表达式中正确的有( ) 如图,用与水平方向夹角为?=37o的恒力 F 拉一质量为 52kg 的物体,使它水平匀速移动 10m,若物体与地面间的动摩擦因数为 ?=0.4,取 g=10m/s 2.求此过程中:
如图,用与水平方向夹角为?=37o的恒力 F 拉一质量为 52kg 的物体,使它水平匀速移动 10m,若物体与地面间的动摩擦因数为 ?=0.4,取 g=10m/s 2.求此过程中: