题目内容
甲车以2m/s的速度做匀速直线运动.出发12s后,乙车从同一地点由静止开始以2m/s2的加速度向同一方向做匀加速直线运动.求:
(1)乙车出发后经多长时间才能追上甲车?
(2)甲、乙两车相遇前的最大距离是多少?
解:(1)乙车出发后经t时间能追上甲车
此时甲车的位移x1=v1(t+12)=2×(t+12)①
乙车的位移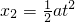 ②
②
乙车出发后追上甲车的位移关系:x1=x2 ③
①②③联立代入数据得:t=6s
(2)当两车速度相等时,相距最远.
有v=at′,则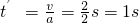 ④
④
此时甲车的位移x1′=v(t′+12)=2×13m=26m
乙车的位移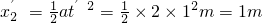
两车相距的最远距离△x=x1′-x2′=26-1m=25m
答:乙车出发后经6s才能追上甲车,甲、乙两车相遇前的最大距离是25m.
分析:(1)当甲乙两车再次相遇时,位移相等,根据位移关系,结合运动学中的位移公式求出乙车追上甲车的时间.
(2)两车速度相等之前,甲车的速度大于乙车的速度,两车之间的距离逐渐增大,两车的速度相等之后,甲车的速度小于乙车的速度,两车之间的距离逐渐减小,当两车的速度相等时,两车之间的距离最远.根据速度相等,求出时间,再根据位移公式求出相距的最远距离.
点评:本题是速度时间关系公式和位移时间关系公式运用的基本问题,关键要熟悉运动学公式,可以结合速度时间关系图象分析,也可画出运动草图.
此时甲车的位移x1=v1(t+12)=2×(t+12)①
乙车的位移
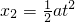 ②
②乙车出发后追上甲车的位移关系:x1=x2 ③
①②③联立代入数据得:t=6s
(2)当两车速度相等时,相距最远.
有v=at′,则
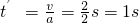 ④
④此时甲车的位移x1′=v(t′+12)=2×13m=26m
乙车的位移
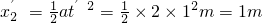
两车相距的最远距离△x=x1′-x2′=26-1m=25m
答:乙车出发后经6s才能追上甲车,甲、乙两车相遇前的最大距离是25m.
分析:(1)当甲乙两车再次相遇时,位移相等,根据位移关系,结合运动学中的位移公式求出乙车追上甲车的时间.
(2)两车速度相等之前,甲车的速度大于乙车的速度,两车之间的距离逐渐增大,两车的速度相等之后,甲车的速度小于乙车的速度,两车之间的距离逐渐减小,当两车的速度相等时,两车之间的距离最远.根据速度相等,求出时间,再根据位移公式求出相距的最远距离.
点评:本题是速度时间关系公式和位移时间关系公式运用的基本问题,关键要熟悉运动学公式,可以结合速度时间关系图象分析,也可画出运动草图.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目