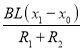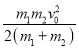Question

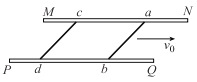
【题目】如图所示，水平光滑的桌面上有一质量M=4kg的长木板静止在光滑水平面上，质量m=1kg的小滑块置于长木板左端，小滑块可视为质点。长木板右侧与固定竖直挡板间的距离L=10m，小滑块以v0=10m/s的速度向右滑上长木板，经过一段时间后，长木板与竖直挡板发生碰撞，碰撞过程无机械能损失。已知小滑块与长木板间的动摩擦因数μ=0.4，重力加速度g=10m/s2，长木板足够长，小滑块始终未脱离长木板。求：

(1)经过多长时间，长木板与竖直挡板相碰？

(2)长木板与竖直挡板碰撞后，小滑块和长木板相对静止时，小滑块距长木板左端的距离。

Answer 1

【答案】(1)6s；(2)11.6m

【解析】

(1)小滑块刚滑上长木板后，小滑块和长木板水平方向动量守恒

mv0=(m+M)v

解得

v=2m/s

对长木板

μmg=Ma

得长木板的加速度

a=1m/s2

自小滑块刚滑上长木板至两者达相同速度

v=at1

解得

t1=2s

长木板位移

解得

x=2m<L=10m.

两者达相同速度时长木板还没有碰竖直挡板，此后两者一起匀速运动，则

L－x=vt2

解得

t2=4s

则总时间为

t=t1+t2=6s

(2)长木板碰竖直挡板后，小滑块和长木板水平方向动量守恒

mv－Mv=(m+M)v′

最终两者的共同速度

由能量守恒定律得

小滑块和长木板相对静止时，小滑块距长木板左端的距离

s=11.6m