题目内容
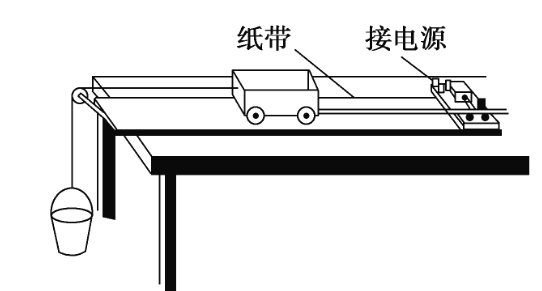
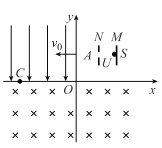
【题目】如图所示，两根间距为L、电阻不计、足够长的光滑平行金属导轨MN、PQ水平故置。导轨所在空间存在方向与导轨所在平面垂直、磁感应强度大小为B的匀强磁场。平行金属杆ab、cd的质量分别为m1、m2，电阻分别为R1、R2，长度均为L， 且始终与导轨保持垂直。初始时两金属杆均处于静止状态，相距为x0。现给金属杆ab一水平向右的初速度v0，一段时间后，两金属杆间距稳定为x1，下列说法正确的是（ ）
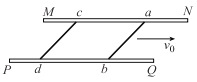
A.全属杆cd先做匀加速直线运动，后做匀速直线运动
B.当全属杆ab的加速度大小为a时，金属杆cd的加速度大小为
C.在整个过程中通过金属杆cd的电荷量为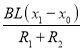
D.金属杆ab、cd运动过程中产生的焦耳热为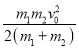
【答案】CD
【解析】
A．因为最终两金属杆保持稳定状态，所以最终两金属杆所受的安培力均为零，即回路中无感应电流，穿过回路的磁通量不再改变，则两金属杆最终的速度相同，所以金属杆ab先做加速度逐渐减小。的减速直线运动，最后做匀速直线运动，金属杆cd先做加速度逐渐减小的加速直线运动，最后做匀速直线运动，A项错误；
B．两金属杆中的电流大小始终相等，根据安培力公式F安=BIL可知两金属杆所受的安培力大小时刻相等，再根据牛顿第二定律F=ma可知当金属杆ab的加速度大小为a时，金属杆cd的加速度大小为
，B项错误；
C．设从金属杆ab获得一水平向右的初速度v0到最终达到共同速度所用的时间为t。则在这段时间内，回路中的磁通量的变化量
= BL（x1-x0）
根据法拉第电磁感应定律有
由闭合电路欧姆定律有
设在这段时间内通过金属杆cd的电荷量为q，所以有
联立以上各式解得
q=
C项正确；
D．设两金属杆最终的共同速度为v，根据动量守恒定律有
设金属杆ab、cd产生的焦耳热为Q，则由能量守恒定律有
解得
Q=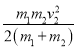
D项正确。
故选CD。
