Question

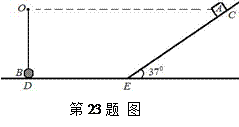
如图所示，小球B用轻绳悬挂于O点，球B恰好与水平地面D点接触，水平地面与斜面连接处E可视为一小段圆弧，水平地面DE部分长度L=3.5m。一质量为m的滑块A（可视为质点）从倾角370、高度h =3m的斜面上C点由静止释放，并在水平面上与B球发生弹性碰撞。已知滑块A与接触面的动摩擦因数均是μ = 0.2，O点与C点在同一水平面上，小球B与滑块A质量相等（sin370=0.6，cos370=0.8，g = 10m/s2）。试求：

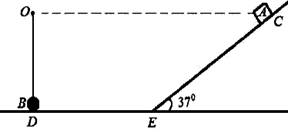
（1）B球与A球第一次碰撞后，A球摆动的最大偏角；

（2）B球第1次回到斜面上的高度；

（3）B球最终的位置到E处的距离。

 

Answer 1

【答案】

略

【解析】

mv2/2=mv21/2+mv22/2----------------------- 1分

v2 = v ，v1=0

mv22/2=mgR(1－cosθ)

θ=600--------------------------------1分

（2）mv22/2=μmgL+μmgcos370x2+ mgh1 -------------4分

x2=h1/sin370

 h1= 0.63m          ----------1分

（3）mgh1－μmgcos370x2－μmgx = 0----4分

x= 2.3 m           ------------1分