题目内容
【题目】如图在水平轨道右侧固定半径为R的竖直圆槽形光滑轨道，水平轨道PQ段铺设特殊材料，调节其初始长度为l，水平轨道左侧有一轻质弹簧左端固定，弹簧处于自然伸长状态。可视为质点的小物块从轨道右侧A点以初速度v0冲上轨道，通过圆形轨道、水平轨道后压缩弹簧，并被弹簧以原速率弹回。已知R＝0.4 m，l＝2.5 m，v0＝6 m/s，物块质量m＝1 kg，与PQ段间的动摩擦因数μ＝0.4，轨道其它部分摩擦不计。取g＝10 m/s2。求：
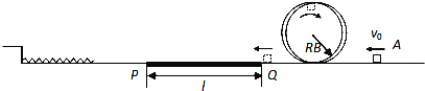
（1）物块经过圆轨道最高点B时对轨道的压力；
（2）物块从Q运动到P的时间及弹簧获得的最大弹性势能；
（3）物块仍以v0从右侧冲上轨道，调节PQ段的长度l，当l长度是多少时，物块恰能不脱离轨道返回A点继续向右运动。
【答案】（1）40N；
（2）8J；
（3）1m．
【解析】
试题(1)物块冲上圆形轨道最高点B时速度为v，由机械能守恒得：
①
物块到B点，由牛顿运动定律得：
②
联立①②式并代入数据解得N=40N ③
由牛顿第三定律，物块对轨道压力大小为40N，方向为竖直向上 ④
(2)物块在Q点时速度为v0＝6 m/s，在PQ运动时，由牛顿运动定律有：
⑤
由运动规律
⑥
联立⑤⑥式并代入数据解得在PQ段运动时间 t=
s ⑦
设物块在P点时速度为v1，有
⑧
由能量守恒，物块压缩弹簧，动能转化为弹性势能，有
⑨
联立⑧⑨式代入数据解得Epm= 8J ⑩
(3)物块以v0冲上轨道直到回到PQ段右侧Q点时速度为v2，有
11
要使物块恰能不脱离轨道返回A点，则物块能沿轨道上滑至最高点且在最高点的速度大小为v3，则满足
12
且
13
联立111213式代入数据解得l＝1 m， 14
练习册系列答案
阅读快车系列答案
相关题目
