题目内容
16.与打点计时器一样,光电计时器也是一种研究物体运动情况时常用的计时仪器,如图甲所示:a、b分别是光电门的激光发射器和接收装置.现利用如图乙所示的装置验证滑块所受外力做功与其动能变化的关系.方法是:在滑块上安装一遮光板,把滑块放在水平放置的气垫导轨上(滑块在该导轨上运动时所受阻力可忽略),通过跨过定滑轮的细绳与钩码相连,连接好1、2两个光电门,在图示位置释放滑块后,光电计时器记录下滑块上的遮光板先后通过两个光电门的时间分别为△t1、△t2.已知滑块(含遮光板)质量为M、钩码质量为m、两光电门间距为s、遮光板宽度为L、当地的重力加速度为g
(1)用游标卡尺(20分度)测量遮光板宽度,刻度如图丙所示,读数为5.70mm
(2)本实验想用钩码的重力表示滑块受到的合外力,为减小这种做法带来的误差,实验中需要满足的条件是M远大于m(填“远大于”“小于”“远小于”)
(3)计算滑块先后通过两个光电门时的瞬时速度的表达式为:v1=$\frac{L}{△{t}_{1}}$、v2=$\frac{L}{△{t}_{2}}$(用题中的字母表示)
(4)本实验中,验证滑块运动的动能定理的表达式为mgs=$\frac{1}{2}$M($\frac{L}{△{t}_{2}}$)2-$\frac{1}{2}$M($\frac{L}{△{t}_{1}}$)2.(用题中所给字母表示)
分析 (1)游标卡尺的读数等于主尺读数加上游标读数,不需估读.
(2)滑块在水平木板运动时水平方向上受到绳的拉力和摩擦力,想用钩码的重力表示小车受到的合外力,首先需要平衡摩擦力;其次:必须要满足钩码的质量远小于滑块的总质量.
(3、4)根据极短时间内的平均速度表示瞬时速度求出滑块先后通过两个光电门的瞬时速度.抓住滑块重力势能的减小量等于滑块动能的增加量列出表达式.
解答 解:(1)游标卡尺的主尺读数为5mm,游标读数为0.05×14mm=0.70mm,则最终读数为5+0.70=5.70mm.
(2)由于滑块在运动的过程中受到阻力,为了减小阻力的影响,需平衡摩擦力.
设钩码的质量为m,滑块的质量为M,对系统运用牛顿第二定律得:a=$\frac{mg}{m+M}$,
则绳子的拉力T=Ma=$\frac{Mmg}{M+m}$=$\frac{mg}{1+\frac{m}{M}}$,当m<<M时,绳子的拉力等于钩码的重力.
(3)滑块通过光电门1的瞬时速度v1=$\frac{L}{△{t}_{1}}$,
通过光电门2的瞬时速度v2=$\frac{L}{△{t}_{2}}$.
(4)滑块重力势能的减小量为mgs,滑块动能的增加量为$\frac{1}{2}$M($\frac{L}{△{t}_{2}}$)2-$\frac{1}{2}$M($\frac{L}{△{t}_{1}}$)2.
则滑块的机械能守恒的表达式为mgs=$\frac{1}{2}$M($\frac{L}{△{t}_{2}}$)2-$\frac{1}{2}$M($\frac{L}{△{t}_{1}}$)2.
故答案为:(1)5.70;
(2)远大于,
(3)$\frac{L}{△{t}_{1}}$,$\frac{L}{△{t}_{2}}$;
(4)mgs=$\frac{1}{2}$M($\frac{L}{△{t}_{2}}$)2-$\frac{1}{2}$M($\frac{L}{△{t}_{1}}$)2.
点评 解决本题的关键掌握螺旋测微器和游标卡尺的读数方法,以及掌握用钩码重力表示小车所受合力的处理方法.
知道极短时间内的平均速度可以表示瞬时速度,以及掌握该实验的原理,明确如何验证动能定理.

 有一个带负电的粒子,从一条电场线上的A点以某一初速度射出,仅在电场力作用下沿该电场线运动到B点,其电势能EP随位移x变化的关系如图所示,则下列说法正确的是( )
有一个带负电的粒子,从一条电场线上的A点以某一初速度射出,仅在电场力作用下沿该电场线运动到B点,其电势能EP随位移x变化的关系如图所示,则下列说法正确的是( )| A. | 该电场不可能是匀强电场 | B. | 粒子运动的速度越来越大 | ||
| C. | 粒子运动的加速度越来越大 | D. | 粒子运动的轨迹为曲线 |
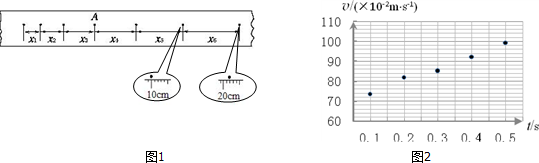
 如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )
如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )| A. | vb=2$\sqrt{2}$m/s | B. | vc=3m/s | ||
| C. | xde=3m | D. | 从d到e所用时间为4s |
| A. | 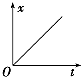 | B. | 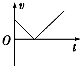 | C. | 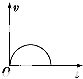 | D. |  |
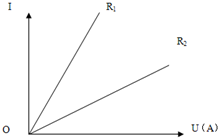 现有电阻R1、R2,它们的电流和电压间关系表示在图中,当它们两端电压相等时,电阻R1和R2所消耗的功率分别为P1、P2,则可知( )
现有电阻R1、R2,它们的电流和电压间关系表示在图中,当它们两端电压相等时,电阻R1和R2所消耗的功率分别为P1、P2,则可知( )| A. | R1>R2,P1>P2 | B. | R1>R2,P1<P2 | C. | R1<R2,P1>P2 | D. | R1<R2,P1<P2 |
| A. | 物体所受的重力就是地球对物体产生的吸引力,方向总是指向地心 | |
| B. | 用细线将重物悬挂起来,静止时物体的重心一定在悬线所在的直线上 | |
| C. | 重心就是物体所受重力的等效作用点,故重心一定在物体上 | |
| D. | 形状规则的物体其重心一定在几何中心 |
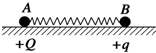 如图所示,真空中A、B两个点电荷的电荷量分别为+Q和+q,放在光滑绝缘水平面上,A、B之间用绝缘的轻弹簧连接.当系统平衡时,弹簧的伸长量为x0.若弹簧发生的均是弹性形变,则( )
如图所示,真空中A、B两个点电荷的电荷量分别为+Q和+q,放在光滑绝缘水平面上,A、B之间用绝缘的轻弹簧连接.当系统平衡时,弹簧的伸长量为x0.若弹簧发生的均是弹性形变,则( )| A. | 保持q不变,将Q变为-Q,平衡时弹簧的压缩量小于x0 | |
| B. | 保持Q不变,将q变为-q,平衡时弹簧的压缩量大于x0 | |
| C. | 保持Q不变,将q变为2q,平衡时弹簧的伸长量等于2x0 | |
| D. | 保持q不变,将Q变为2Q,平衡时弹簧的伸长量大于2x0 |