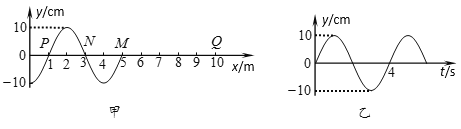
题目内容
【题目】单色细光束射到一半径为R的透明球表面,光线在过球心的平面内,入射角i=45°,经折射进入球内后又经内表面反射一次,再经球表面折射后射出,已知真空中光速为c,入射光线与出射光线反向延长线之间的夹角α=30°,如图所示(图上已画出入射光线和出射光线)
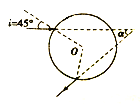
①求透明球对该单色光的折射率;
②光在透明球中传播的时间。
【答案】①![]() ②
②![]()
【解析】①连接圆心O与角α的顶点,交球面于C点,连接AC、CB,ACB即为光线的路径,如图所示.
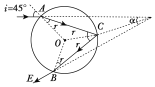
由几何关系及对称性,有:r=![]() +(i-r)
+(i-r)
解得:r=30°
由折射定律得: ![]()
②由几何关系得:AC=BC=2Rcosr= ![]()
光在透明球中传播路程为:L=2![]() R
R
光在透明球中传播的速度为: ![]()
光在透明球中传播的时间为: ![]()

练习册系列答案
相关题目