题目内容
【题目】质量为M的小车固定在地面上，质量为m的小物体（可视为质点）以v0的水平速度从小车一端滑上小车，小物体从小车另一端滑离小车时速度减为
，已知物块与小车之间的动摩擦因数为
.求：
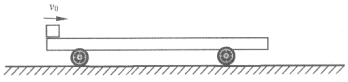
（1）此过程中小物块和小车之间因摩擦产生的热Q以及小车的长度L.
（2）若把同一小车放在光滑的水平地面上，让这个物体仍以水平速度v0从小车一端滑上小车.
a. 欲使小物体能滑离小车，小车的质量M和小物体质量m应满足什么关系?
b. 当M=4m时，小物块和小车的最终速度分别是多少?
【答案】（1）
，
（2）a. M>3m；b. 
，
【解析】
(1) 小车固定在地面时，物体与小车间的滑动摩擦力为
，
物块滑离的过程由动能定理
①
解得：
物块相对小车滑行的位移为L，摩擦力做负功使得系统生热，
可得：
（2）a.把小车放在光滑水平地面上时，小物体与小车间的滑动摩擦力仍为f．
设小物体相对小车滑行距离为
时，跟小车相对静止（未能滑离小车）共同速度为v，
由动量守恒定律：
mv0=(M+m)v ②
设这过程小车向前滑行距离为s.
对小车运用动能定理有:
③
对小物体运用动能定理有:
④
联立②③④可得
⑤
物块相对滑离需满足
且
联立可得：
，
即小物体能滑离小车的质量条件为
b.当M=4m时满足，则物块最终从小车右端滑离，设物块和车的速度分别为
、
.
由动量守恒：
由能量守恒定律：
联立各式解得：
，
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
