题目内容
如图所示,一小球从A点以某一水平向右的初速度出发,沿水平直线轨道运动到B点后,进入半径R=10cm的光滑竖直圆形轨道,圆形轨道间不相互重叠,即小球离开圆形轨道后可继续向C点运动,C点右侧有一壕沟,C、D两点的竖直高度h=0.8m,水平距离s=1.2m,水平轨道AB长为L1=1m,BC长为L2=3m,.小球与水平轨道间的动摩擦因数μ=0.2,重力加速度g=10m/s2,则:
(1)若小球恰能通过圆形轨道的最高点,求小球在A点的初速度?
(2)若小球既能通过圆形轨道的最高点,又不掉进壕沟,求小球在A点的初速度的范围是多少?
(1)vA=3m/s(2)3m/s≤vA≤4m/s和vA≥5m/s
解析:(1)小球恰能通过圆形轨道的最高点,mg=mv2/R,
由B到最高点,机械能守恒,![]() mvB2=
mvB2=![]() mv2+mg·2R
mv2+mg·2R
由A到B,由动能定理,-μmgL1=![]() mvB2-
mvB2-![]() mvA2
mvA2
联立解得小球在A点的初速度vA=3m/s。
(2)若小球刚好停在C处,则有-μmg(L1+L2)=-![]() mv’A2
mv’A2
解得,v’A=4m/s。
若小球刚好停在BC段,则有3m/s≤vA≤4m/s。
若小球能通过C点,并越过壕沟,则有h=![]() gt2,s=vCt,
gt2,s=vCt,
由动能定理,-μmg(L1+L2)= ![]() mvC2-
mvC2-![]() mvA2
mvA2
联立解得:vA=5m/s。
小球既能通过圆形轨道的最高点,又不掉进壕沟,小球在A点的初速度的范围是:
3m/s≤vA≤4m/s和vA≥5m/s。

练习册系列答案
相关题目
 如图所示,一小球从A点由静止开始沿斜面做匀变速直线运动,若到达B点时速度为v,到达C点时速度为2v,则AB:BC等于( )
如图所示,一小球从A点由静止开始沿斜面做匀变速直线运动,若到达B点时速度为v,到达C点时速度为2v,则AB:BC等于( ) (2010?平顶山模拟)如图所示,一小球从A点以某一水平向右的初速度出发,沿水平直线轨道运动到B点后,进入半径R=10cm的光滑树枝圆形轨道,圆形轨道间不相互重叠,即小球离开圆形轨道后可继续向C点右侧有一壕沟,C、D两点的竖直高度h=0.8cm,水平距离s=1.2cm,水平轨道AB长为L1=1m,BC长为L2=3m.小球与水平轨道间的动摩擦因数u=0.2,重力加速度g=10m/s2,重力加速度g=10m/s2,则:
(2010?平顶山模拟)如图所示,一小球从A点以某一水平向右的初速度出发,沿水平直线轨道运动到B点后,进入半径R=10cm的光滑树枝圆形轨道,圆形轨道间不相互重叠,即小球离开圆形轨道后可继续向C点右侧有一壕沟,C、D两点的竖直高度h=0.8cm,水平距离s=1.2cm,水平轨道AB长为L1=1m,BC长为L2=3m.小球与水平轨道间的动摩擦因数u=0.2,重力加速度g=10m/s2,重力加速度g=10m/s2,则:

 的光滑竖直圆形轨道,圆形轨道间不相互重叠,即小球离开圆形轨道后可继续向C点运动,C点右侧有一壕沟,C、D两点的竖直高度
的光滑竖直圆形轨道,圆形轨道间不相互重叠,即小球离开圆形轨道后可继续向C点运动,C点右侧有一壕沟,C、D两点的竖直高度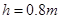 ,水平距离
,水平距离 ,水平轨道AB长为
,水平轨道AB长为 ,BC长为
,BC长为 ,小球与水平轨道间的动摩擦因数
,小球与水平轨道间的动摩擦因数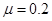 ,重力加速度
,重力加速度 .求:
.求: