题目内容
如图所示,一根轻杆长1m,可绕O轴在竖直平面内无摩擦地转动,OA=0.6m,OB=0.4m,质量相等的两小球分别固定于杆的A、B两端,现把杆位于水平位置,然后自由释放,求轻杆转到竖直位置时两球的速度分别是多少?
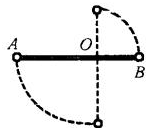

在转动过程中,A、C两球的角速度相同,设A球的速度为vA,B球的速度为vB,则有:
3vA=2vB…①
以A、B和杆组成的系统机械能守恒,由机械能守恒定律,并选水平为零势能参考平面,则有:
E1=0,
E2=mg?OB-mg?OA+
mvA2+
m
E1=E2
即0=mg?OB-mg?OA+
mvA2+
m
…②
结合①②两式,代入数值OA=0.6m,OB=0.4m
得:vA=
vB=
答:轻杆转到竖直位置时,A、B两球的速度分别是
,
.
3vA=2vB…①
以A、B和杆组成的系统机械能守恒,由机械能守恒定律,并选水平为零势能参考平面,则有:
E1=0,
E2=mg?OB-mg?OA+
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2B |
E1=E2
即0=mg?OB-mg?OA+
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2B |
结合①②两式,代入数值OA=0.6m,OB=0.4m
得:vA=
|
vB=
|
答:轻杆转到竖直位置时,A、B两球的速度分别是
|
|

练习册系列答案
相关题目