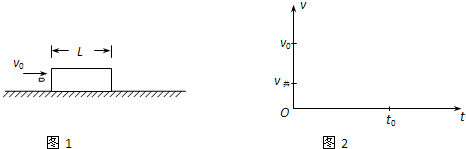题目内容
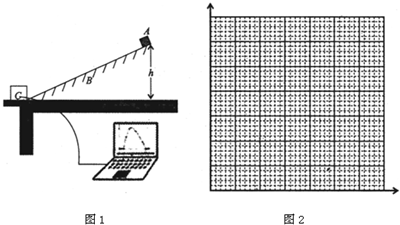
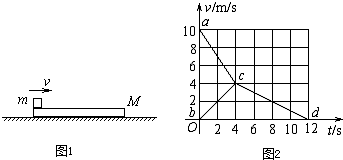
如图1所示,质量为M的长木板,静止放置在粗糙水平地面上,有一个质量为m、可视为质点的物块,以某一水平初速度从左端冲上木板.从物块冲上木板到物块和木板达到共同速度的过程中,物块和木板的v-t图象分别如图2中的折线acd和bcd所示,a、b、c、d点的坐标为a(0,1.0)、b(0,0)、c(4,0.4)、d(l2,0).根据v-t图象,求:
(1)物块在长木板上滑行的距离;
(2)物块质量m与木板质量M之比.

(1)物块在长木板上滑行的距离;
(2)物块质量m与木板质量M之比.
分析:(1)物块滑上长木板后,做匀减速直线运动,长木板做匀加速直线运动,当两者速度相同后,一起做匀减速直线运动.根据图线与时间轴围成的面积分别求出物块在达到共同速度前木块和长木板的位移,从而求出位移之差,即物块在长木板上 滑行的距离.
(2)分别对物块、木板和整体运用牛顿第二定律,结合图线求出加速度的大小,从而得出木块和木板的质量之比.
(2)分别对物块、木板和整体运用牛顿第二定律,结合图线求出加速度的大小,从而得出木块和木板的质量之比.
解答:解:(1)由v-t图象的物理意义可得,物块在木板上滑行的距离△s=
×4m-
×4m=20 m
(2)设物块冲上木板做匀减速直线运动的加速度大小为a1,木板做匀加速直线运动的加速度大小为a2,达相同速度后一起匀减速直线运动的加速度大小为a,
根据牛顿第二定律对物块,μ1mg=ma1①
对木板:μ1mg-μ2(m+M)g=Ma2 ②
对整体:μ2(m+M)g=(M+m)a ③
由图象得,a1=1.5m/s2,a2=1m/s2,a=0.5m/s2.
由以上各式解得
=
.
答:(1)物块在长木板上滑行的距离为20m.
(2)物块质量m与木板质量M之比为3:2.
| 10+4 |
| 2 |
| 4 |
| 2 |
(2)设物块冲上木板做匀减速直线运动的加速度大小为a1,木板做匀加速直线运动的加速度大小为a2,达相同速度后一起匀减速直线运动的加速度大小为a,
根据牛顿第二定律对物块,μ1mg=ma1①
对木板:μ1mg-μ2(m+M)g=Ma2 ②
对整体:μ2(m+M)g=(M+m)a ③
由图象得,a1=1.5m/s2,a2=1m/s2,a=0.5m/s2.
由以上各式解得
| m |
| M |
| 3 |
| 2 |
答:(1)物块在长木板上滑行的距离为20m.
(2)物块质量m与木板质量M之比为3:2.
点评:解决本题的关键理清物块和木板的运动情况,结合牛顿第二定律和图象进行求解.知道图线与时间轴围成的面积表示位移,图线的斜率表示加速度.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目