题目内容
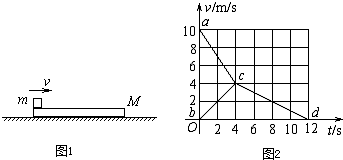
如图1所示,质量为M的木块静止在光滑水平面上,一质量为m的子弹以速度v0水平射入木块,子弹恰好未从木块中射出.设木块对子弹的阻力为恒力,其大小为F.
(1)求木块的长度L;
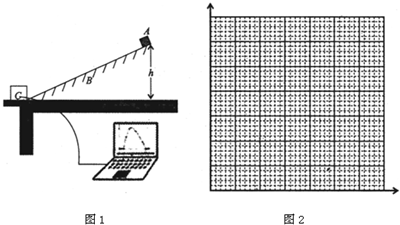
(2)如果其他条件不变,只是将木块固定在水平面上,以子弹射入木块时为计时起点,以t0表示子弹运动到木块最右端的时刻,请你在下面给出的坐标系中(如图2)定性画出子弹在0~t0这段时间内的速度随时间变化的图线.(图中标出了子弹的初速度v0和未固定木块时子弹与木块的共同速度v共.)
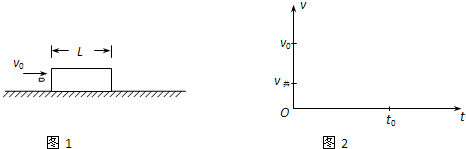
(1)求木块的长度L;
(2)如果其他条件不变,只是将木块固定在水平面上,以子弹射入木块时为计时起点,以t0表示子弹运动到木块最右端的时刻,请你在下面给出的坐标系中(如图2)定性画出子弹在0~t0这段时间内的速度随时间变化的图线.(图中标出了子弹的初速度v0和未固定木块时子弹与木块的共同速度v共.)
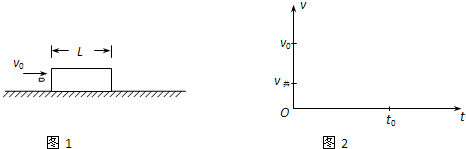
分析:(1)根据动量守恒定律求出木块和子弹最终的速度,设木块的位移为x,根据运动学公式列出子弹和木块的速度位移关系式,根据牛顿第二定律求出两者加速度的关系,联合求解得出L.本题也可以根据功能关系进行求解.
(2)如果将木块固定,可知子弹将穿出木块,根据能量守恒知道子弹射出木块的速度大于木块不固定时的共同速度.子弹在木块中做匀减速直线运动.
(2)如果将木块固定,可知子弹将穿出木块,根据能量守恒知道子弹射出木块的速度大于木块不固定时的共同速度.子弹在木块中做匀减速直线运动.
解答: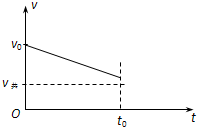 解:(1)设子弹与木块的共同速度为v
解:(1)设子弹与木块的共同速度为v
mv0=(m+M)v①
设子弹与木块相互作用过程中,木块的位移为x
以子弹为研究对象v2=v02-2a1(x+L)②
a1=
③
以木块为研究对象v2=2a2x④
a2=
⑤
由以上各式解得L=
⑥
(2)将木块固定在水平桌面上,则子弹将穿出木块,穿出木块的速度大于木块不固定时的共同速度.
子弹在木块中做初速度为v0的匀减速直线运动,最终的末速度大于v共.
图线如图.
答:(1)木块的长度L为L=
.
(2)如图.
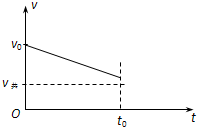 解:(1)设子弹与木块的共同速度为v
解:(1)设子弹与木块的共同速度为vmv0=(m+M)v①
设子弹与木块相互作用过程中,木块的位移为x
以子弹为研究对象v2=v02-2a1(x+L)②
a1=
| F |
| m |
以木块为研究对象v2=2a2x④
a2=
| F |
| M |
由以上各式解得L=
| Mmv02 |
| 2F(M+m) |
(2)将木块固定在水平桌面上,则子弹将穿出木块,穿出木块的速度大于木块不固定时的共同速度.
子弹在木块中做初速度为v0的匀减速直线运动,最终的末速度大于v共.
图线如图.
答:(1)木块的长度L为L=
| Mmv02 |
| 2F(M+m) |
(2)如图.
点评:本题考查了动量守恒定律、牛顿第二定律以及运动学中速度位移关系式,综合性较强,难度中等.本题也可以采取功能关系进行解决.

练习册系列答案
相关题目