题目内容
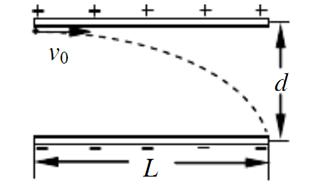
(14分)如图所示,在同一平面内边长均为l的正方形区域abcd和cdef中.分别存在平行于ab方向的匀强电场和垂直纸面向里的匀强磁场.质量为m电荷量为q的带电粒子,以速度υ0沿ad方向从a点射入电场,并从dc边的中点O射出,不计重力.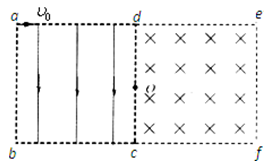
(1)求电场强度的大小;
(2)若粒子垂直于ef边界射出磁场,求它在电、磁场中运动的总时间;
(3)磁场的磁感应强度大小在什么范围内时,粒子才能从de边界射出磁场?
(1)  ;(2)
;(2)  ;(3)
;(3) 
解析试题分析:(1)粒子在偏转电场中仅受竖直向下的电场力,做类平抛运动,
水平方向做匀速直线运动:L=v0t1
竖直方向做初速度为零匀加速直线运动: ;
;
整理得:
(2)粒子离开电场时的末速度可以分解为水平分速度v0与竖直分速度vy,设v与v0之间的夹角为θ
则: ;
;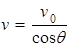 解得:
解得:
粒子进入磁场后做匀速圆周运动,垂直于ef边界射出磁场是的丶轨迹如图.由几何关系知:rsinθ=L
粒子经过磁场区域的时间:
粒子通过电磁场的总时间:t=t1+t2=

(3)档粒子运动的轨迹与ef相切时,根据几何关系得: r1sinθ+r1=L
根据牛顿第二定律得: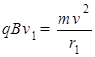
解得: 
当粒子与边界de相切时,根据几何关系得:r1sinθ+r1= L
L
根据牛顿第二定律可得: ;解得
;解得 ;
;
故 ,得:
,得:
考点:带电子粒子在匀强电场及在匀强磁场中的运动.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案如图所示,匀强磁场的方向垂直于光滑的金属导轨平面向里,极板间距为d的平行板电容器与总阻值为2R0的滑动变阻器通过平行导轨连接,电阻为R0的导体棒MN可在外力的作用下沿导轨从左向右做匀速直线运动。当滑动变阻器的滑动触头位于a、b的中间位置且导体棒MN的速度为v0时,位于电容器中P点的带电油滴恰好处于静止状态。若不计摩擦和平行导轨及导线的电阻,各接触处接触良好,重力加速度为g,则下列判断正确的是
| A.油滴带正电荷 |
| B.若将上极板竖直向上移动距离d,油滴将向上加速运动,加速度a = g/2 |
| C.若将导体棒的速度变为2v0,油滴将向上加速运动,加速度a = g |
| D.若保持导体棒的速度为v0不变,而将滑动触头置于a端,同时将电容器上极板向上移动距离d/3,油滴仍将静止 |



 =1×108 C/kg、初速度为v0=2×105 m/s的带正电粒子。忽略粒子重力以及它们之间的相互作用.
=1×108 C/kg、初速度为v0=2×105 m/s的带正电粒子。忽略粒子重力以及它们之间的相互作用. 
 的电子从
的电子从 点沿与电场垂直的方向进入匀强电场,初速度为
点沿与电场垂直的方向进入匀强电场,初速度为 ,当它通过电场中
,当它通过电场中 点时,速度与场强方向成
点时,速度与场强方向成 角,不计电子的重力,求:
角,不计电子的重力,求:
 两点间的电势差多大。
两点间的电势差多大。