��Ŀ����
����Ŀ���������ΪL���㹻���Ľ���ֱ�ǵ�����ͼ��ʾ���ã����Ǹ���һ������ͬһˮƽ���ڣ���һ���ִ�ֱ��ˮƽ�森������Ϊm�Ľ���ϸ��ab��cd�뵼�촹ֱ�Ӵ��γɱպϻ�·�����뵼��֮��Ķ�Ħ��������Ϊ�̣�������費�ƣ���·�ܵ���Ϊ2R������װ�ô��ڴŸ�Ӧǿ�ȴ�СΪB��������ֱ���ϵ���ǿ�ų��У���ab����ƽ����ˮƽ���������F���������ٶ�v1�ص��������˶�ʱ��cd��Ҳ�������ٶ�v2���������˶����������ٶ�Ϊg������˵������ȷ���ǣ� ��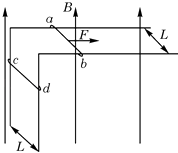
A.ab����������F�Ĵ�СΪ ![]() +��mg
+��mg
B.cd������Ħ����Ϊ��
C.��·�еĵ���ǿ��Ϊ ![]()
D.����v1��С�Ĺ�ϵΪ��= ![]()
���𰸡�A,D
���������⣺A�������и�Ÿ���ʱ������abdca����ĸ�Ӧ��������СΪ��I= ![]() ��
��
����ab�ܵ�ˮƽ����İ�������������ƽ��ã�BIL+mg��=F ��
�����cd�˶�ʱ������ֱ�����ܵ�Ħ����������ƽ�⣬�У�f=BIL��=mg ��
�������ϸ�ʽ��ã�F=mg��+ ![]() ����=
����= ![]()
��AD��ȷ��BC����
��ѡAD��
�����㾫�������ڱ��⿼��İ������͵�Ÿ�Ӧ����ѧ����Ҫ�˽ⰲ����������·���йأ��Ʊպϻ�·һ�ܣ����������Ĺ�����Ϊ��������Ϊ����Ҳ����Ϊ�㣬�����������͵糡������������Ϊ�㣻�÷����ڵ�Ÿ�Ӧ���ɺ���ζ������Ӧ�綯�ƵĴ�С�ͷ������·�е���ǿ�ȣ������о�������������������������������ֶ���ȷ���䷽���ж���ѧ���̻�ƽ�ⷽ�������ܵó���ȷ�𰸣�

 �żӾ���ϵ�д�
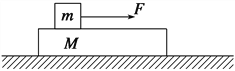
�żӾ���ϵ�д�����Ŀ��ijС�顰��֤ţ�ٵڶ����ɡ���ʵ��װ������ͼ����ľ��̶���ˮƽ�����ϣ�һ��װ�ж����֣�ľ������һ���飬��һ�����Ŵ���ʱ����ֽ����������һ��ͨ����������ֵ�ϸ�����������ӡ�
��1����С���о����ٶȺ�������ϵʱ���õ���ͼ����ͼ

��2����ͼ��������ʵ���л�ȡ��һ��ֽ����һ���֣�1��2��3��4��5��6��7�Ǽ�����ÿ������������仹��4����㣨ͼ��δ��������������ľ�����ͼ��ʾ������ͼ�����ݼ���ļ��ٶ�a= m/s2 ��������λ��Ч��������

��3��ijͬѧ���о����ٶȺ�������ϵʱ����¼���������ݣ��������������ֽ��ѡ����������꣬������ͼ�ߣ���������ͼ�߿��Եõ�ʵ����ۣ� ��
���� | 1 | 2 | 3 | 4 | 5 |
����m/g | 200 | 300 | 400 | 500 | 600 |
���ٶ�a/m�Bs-2 | 1.00 | 0.67 | 0.50 | 0.40 | 0.33 |