��Ŀ����
����Ŀ����ͼ��ʾ���ڹ⻬��Ե��ˮƽ���ϣ��ó�Ϊ2L�ľ�Ե�����������������Ϊm�Ĵ���С��A��B��A��Ĵ�����Ϊ+2q��B��Ĵ�����Ϊ��3q���������һ����ϵͳ������MN��PQƽ�������3L����ʼʱA��B�ֱ�ֹ������MN�����࣬����MNǡΪAB�������ߵĴ�ֱƽ���ߣ�����С��Ϊ�ʵ㣬������˵�������������MN��PQ�����ˮƽ���ҵĵ糡ǿ��ΪE����ǿ�糡������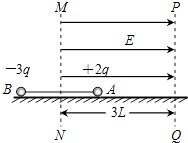
��1��B��ս���糡ʱ������ϵͳ���ٶȴ�С��
��2������ϵͳ�����˶���������ʹ˹�����B������ܵı仯����
��3������ϵͳ�˶������ڣ�
���𰸡�
��1���⣺��B��ս���糡ʱ����ϵͳ���Ϊv1���ɶ��ܶ����� ![]()
��� ![]()
��B��ս���糡ʱ������ϵͳ���ٶȴ�СΪ ![]()
��2���⣺����ϵͳ�����˶������Σ�B�����糡ǰ������ϵͳ�ڵ糡�С�A����糡��
��A���뿪PQ�����λ��Ϊx���ɶ��ܶ�����2qEL��qEL��3qEx=0
��� ![]() ��
�� ![]()
B��Ӹս���糡������ϵͳ�ӿ�ʼ�˶����ٶȵ�һ��Ϊ��ʱλ��Ϊ ![]()
������ܵı仯��Ϊ ![]()
�𣺴���ϵͳ�����˶���������Ϊ ![]() ��B������ܵı仯��Ϊ4qEL��
��B������ܵı仯��Ϊ4qEL��
��3���⣺�����˶������Σ�ȡ����Ϊ������
��һ�μ��� ![]() ��
�� ![]()
�ڶ��μ��� ![]()
��A����糡���ٶ�Ϊv2���ɶ��ܶ����� ![]()
��� ![]() ��
��
�� ![]()
�������ټ���������ٶ�a3��ʱ��t3Ϊ�� ![]() ��
�� ![]()
���Դ���ϵͳ�˶�������Ϊ�� ![]() ��
��
�𣺴���ϵͳ�˶������� ![]()
����������1����ϵͳ���ö��ܶ��������ݶ��ܶ������B��ս���糡ʱ������ϵͳ���ٶȴ�С����2������ϵͳ�����������Σ���B�����糡ǰ������ϵͳ�ڵ糡�С�A����糡�����ݶ��ܶ������A���뿪PQ�����λ�ƣ��Ӷ��������ϵͳ�����˶��������룮����B���ڵ糡���˶���λ�ƣ�����糡�����Ĺ����Ӷ�ȷ��B������ܵı仯������3�������˶�ѧ��ʽ��ţ�ٵڶ����ɷֱ��������ϵͳB�����糡ǰ���ȼ���ֱ���˶���ʱ�䣬����ϵͳ�ڵ糡�����ȼ���ֱ���˶���ʱ�䣬A����糡����ϵͳ���ȼ���ֱ���˶���ʱ�䣬�Ӷ��������ϵͳ�Ӿ�ֹ��ʼ�����˶��ٴ��ٶ�Ϊ���ʱ�䣬����ϵͳ���˶�����Ϊ��ʱ���2����
�����㾫�������ն��ܶ������ۺ�Ӧ���ǽ����ĸ�������Ҫ֪��Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ�

 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�����Ŀ���±��г���ijƷ�Ƶ綯���г�����ͼ�������õ綯������Ҫ����������������������е��ģ����ó��ڶ״̬������������ٶ���ʻ���� ��
���� | 40��kg�� | ���ѹ | 48��V�� |
���� | 75��kg�� | ����� | 12��A�� |
�����ʻ�ٶ� | 20��km/h�� | �������� | 350��W�� |

A.�綯�������빦��Ϊ576 W
B.�綯�����ڵ���Ϊ4��
C.�ó��ܵ�������Ϊ63 N
D.�ó���õ�ǣ����Ϊ104 N