Question

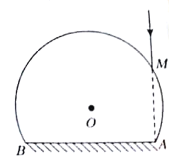
【题目】如图所示，半径为R的玻璃球冠的折射率为，其底面镀银，底面的半径为；在过球心O且垂直于底面的平面内，有一与底面垂直的光线射到玻璃球冠上的M点，该光线的延长线恰好过底面边缘上的A点。已知光在真空中的传播速度为c，不考虑折射时的反射光。求：

①该光线由M点射入玻璃球冠经一次反射后从球面射出的方向相对于其初始入射方向的偏角；

②光在玻璃球冠中的传播时间。

Answer 1

【答案】①150°；②

【解析】

①设球半径为R，球冠底面中心为O′，连接OO′，则OO′⊥AB。令∠OAO′＝α，有

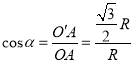
即

α＝30°

由题意

MA⊥AB

所以

∠OAM＝60°

设图中N点为光线在球冠内底面上的反射点，所考虑的光线的光路图如图所示

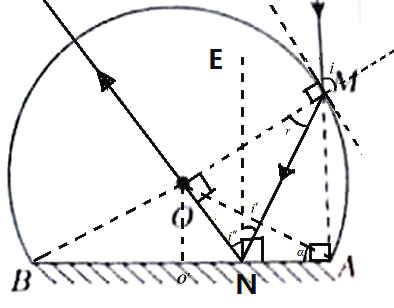
设光线在M点的入射角为i、折射角为r，在N点的入射角为i′，反射角为i″，玻璃折射率为n。由于OAM为等边三角形，有

i＝60°

由折射定律有

sini＝nsinr

代入题给条件

得

作底面在N点的法线NE，由于NE∥AM，有

i′＝30°

根据反射定律，有

i″＝30°

连接ON，由几何关系知

MAN≌MON

故有

∠MNO＝60°

解得

∠ENO＝30°

于是∠ENO为反射角，ON为反射光线。这一反射光线经球面再次折射后不改变方向。所以，经一次反射后射出玻璃球冠的光线相对于入射光线的偏角β为

β＝180°－∠ENO＝150°

②光线在玻璃球冠中的传播速度为

光线在玻璃球冠中的传播时间为

代入数据解得