��Ŀ����
����Ŀ����ͼ��ʾ�����������������Ϊd��������ѹΪU����������ǿ�ų��ĴŸ�Ӧǿ��ΪB1��һ���������ͬ�Ĵ���������Ӵ�ͼʾ�����������������ֱ�ߴ����������������һ�Ÿ�Ӧǿ��ΪB2����ǿ�ų�������ֱ����a��b���㣬��������Ϊ��L����������������Ϊq���Ҳ�������������������
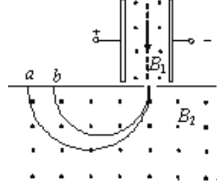
(1)����B2����ǿ�ų�ʱ���ӵ��ٶȣ�
(2)����a��b��������ӵ�����֮����m�Ƕ��٣�
���𰸡�(1)![]() (2)
(2)![]()
��������
��1����������������������糡������������ƽ�⣬����ƽ������������е��ٶ�v��
��2���ڴų�2������������Բ���˶������������ṩԲ���˶������������ݰ뾶��Ĺ�ϵʽ������ӵ��������m
�� ������������ֱ���˶������� qE=B1qv
E=U/d
������ v=U/dB1
�� ���ٶ�v����B2������������Բ���˶�����ţ�ٵڶ����ɵã�
qv B2 =m![]() �� ��
�� ��![]() ��
��![]()
���� ![]()
��ã�![]()

��ϰ��ϵ�д�
 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����Ŀ