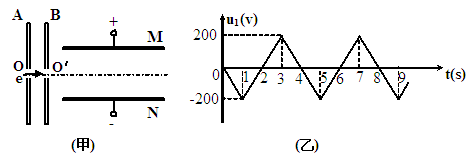题目内容
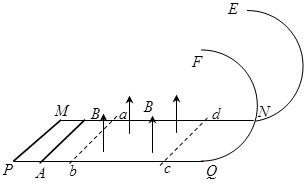
如图所示, 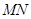 和
和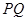 为固定在绝缘水平面上两平行光滑金属导轨,导轨左端
为固定在绝缘水平面上两平行光滑金属导轨,导轨左端 间接有阻值为
间接有阻值为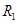 =
=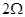 导线;导轨右端接有与水平轨道相切、半径
导线;导轨右端接有与水平轨道相切、半径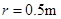 内壁光滑的半圆金属轨道。导轨间距
内壁光滑的半圆金属轨道。导轨间距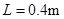 ,电阻不计。导轨所在平面
,电阻不计。导轨所在平面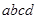 区域内有竖直向上
区域内有竖直向上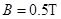 的匀强磁场。导轨上长度也为
的匀强磁场。导轨上长度也为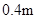 、质量
、质量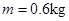 、电阻
、电阻 =
=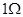 的金属棒
的金属棒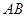 以
以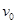 =
=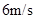 速度进入磁场区域,离开磁场区域后恰好能到达半圆轨道的最高点,运动中金属棒始终与导轨保持良好接触。已知重力加速度
速度进入磁场区域,离开磁场区域后恰好能到达半圆轨道的最高点,运动中金属棒始终与导轨保持良好接触。已知重力加速度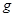 =
= 。求:
。求:
(1)金属棒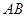 刚滑出磁场右边界
刚滑出磁场右边界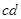 时的速度
时的速度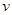 的大小;
的大小;
(2)金属棒滑过磁场区的过程中,导线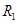 中产生的热量
中产生的热量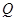 。
。
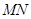 和
和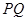 为固定在绝缘水平面上两平行光滑金属导轨,导轨左端
为固定在绝缘水平面上两平行光滑金属导轨,导轨左端 间接有阻值为
间接有阻值为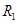 =
=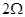 导线;导轨右端接有与水平轨道相切、半径
导线;导轨右端接有与水平轨道相切、半径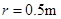 内壁光滑的半圆金属轨道。导轨间距
内壁光滑的半圆金属轨道。导轨间距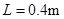 ,电阻不计。导轨所在平面
,电阻不计。导轨所在平面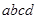 区域内有竖直向上
区域内有竖直向上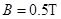 的匀强磁场。导轨上长度也为
的匀强磁场。导轨上长度也为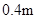 、质量
、质量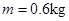 、电阻
、电阻 =
=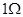 的金属棒
的金属棒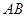 以
以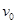 =
=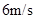 速度进入磁场区域,离开磁场区域后恰好能到达半圆轨道的最高点,运动中金属棒始终与导轨保持良好接触。已知重力加速度
速度进入磁场区域,离开磁场区域后恰好能到达半圆轨道的最高点,运动中金属棒始终与导轨保持良好接触。已知重力加速度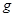 =
= 。求:
。求:
(1)金属棒
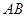 刚滑出磁场右边界
刚滑出磁场右边界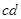 时的速度
时的速度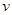 的大小;
的大小;(2)金属棒滑过磁场区的过程中,导线
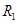 中产生的热量
中产生的热量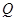 。
。(1)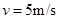 (2)
(2)
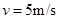 (2)
(2)
试题分析:(1)在轨道的最高点,根据牛顿定律
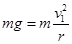 ①
①金属棒刚滑出磁场到最高点,根据机械能守恒
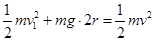 ②
②由①②式代入数据解得
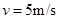 ③
③(2)对金属棒滑过磁场的过程中,根据能量关系
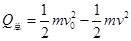 ④
④对闭合回路,根据热量关系
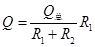 ⑤
⑤由④⑤式并代入数据得
 ⑥
⑥点评:考查的问题较多,但多为基础知识的应用,掌握好法拉第电磁感应定律、安培力、圆周运动及电路的性质即可顺利求解.

练习册系列答案
相关题目
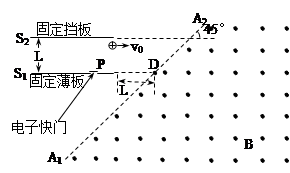
 C/kg。只考虑纸面上带电微粒的运动)
C/kg。只考虑纸面上带电微粒的运动)





 所对应的圆心角为
所对应的圆心角为 。不计离子重力。求:
。不计离子重力。求: