题目内容
17.如图所示,理想变压器原线圈与间距为$\sqrt{2}$m的光滑水平导轨相连,磁感应强度为0.5T的匀强磁场与导轨平面垂直,导线棒与导轨垂直且接触良好,不计导轨和导线棒的电阻.导线棒以OO1位置为平衡位置沿导轨做简谐运动,其位移图象如图,副线圈接一只额定电压为110V的灯泡,灯泡正常发光.下列说法正确的是( )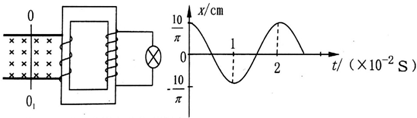
| A. | 0时刻导线棒产生的感应电动势最大 | |
| B. | 原线圈与副线圈的匝数比为1:22 | |
| C. | 导线棒在平衡位置时穿过副线圈的磁通量的变化率最大 | |
| D. | 驱动导线棒的外力的功率始终不变 |
分析 A、0时刻导体棒的速度为零,根据E=BLv判断感应电动势的大小;
B、由图象得到简谐运动的位移表达式,采用微元法得到速度表达式;然后结合公式E=BLv求解电动势的最大值,根据U=$\frac{{U}_{m}}{\sqrt{2}}$求解有效值,最后根据变压比公式求解变压比;
C、导线棒在平衡位置时速度最大,故产生的感应电动势最大,但感应电流的顺势变化率为零;
D、驱动导线棒的外力的功率等于变压器的输入功率的瞬时值.
解答 解:A、t=0时刻,导体棒在最大位移位置,速度为零,故感应电动势为零,故A错误;
B、由x-t图,有:
x=Asin(ωt+$\frac{π}{2}$)=$\frac{10}{π}sin(100πt+\frac{π}{2})cm$
故v=Aωcos(ωt+$\frac{π}{2}$)=1000cos(100πt+$\frac{π}{2}$)cm/s=10cos(100πt+$\frac{π}{2}$)m/s
故输入电压最大值为:${U}_{1m}=BL{v}_{m}=0.5×\sqrt{2}×10$V=5$\sqrt{2}$V
故输入电压的有效值为:${U}_{1}=\frac{{U}_{1m}}{\sqrt{2}}=5V$
灯泡正常发光,故输出电压为:U2=110V
故原副线圈的匝数比为:$\frac{{n}_{1}}{{n}_{2}}=\frac{{U}_{1}}{{U}_{2}}=\frac{5V}{110V}=\frac{1}{22}$;故B正确;
C、导线棒在平衡位置时速度最大,感应电动势最大,但感应电流变化率为零,故导线棒在平衡位置时穿过原、副线圈的磁通量的变化率为零;故C错误;
D、根据P=i2R,驱动导线棒的外力的功率不断变化;故D错误;
故选:B.
点评 本题中导体棒做简谐运动,产生正弦式交变电流,有x-t图象得到位移时间关系和速度时间关系,然后结合公式E=Blv求解电动势的瞬时值进行分析,同时要结合变压器的原理进行分析,不难.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | 先等压膨胀,再等容降温,其温度必低于起始温度 | |
| B. | 先等温膨胀,再等压压缩,其体积必小于起始体积 | |
| C. | 先等容升温,再等压压缩,其温度有可能等于起始温度 | |
| D. | 先等容加热,再绝热压缩,其内能必大于起始内能 |
| A. | 玻尔建立了量子理论,成功解释了各种原子发光现象 | |
| B. | 德布罗意首先提出了物质波的猜想,而电子衍射实验证实了他的猜想 | |
| C. | 比结合能越大表示原子核中的核子结合得越牢固 | |
| D. | β衰变中产生的β射线是原子核外电子挣脱原子核束缚后形成的 | |
| E. | 一个处于n=4能级的氢原子向低能级跃迁时可能只放出三种不同频率的光子 |
| A. | x为质子 | |
| B. | x是钍核中的一个中子转化成一个质子时产生的 | |
| C. | γ射线是镤核从高能级向低能级跃迁时辐射出来的 | |
| D. | 1g钍${\;}_{90}^{234}$Th经过120天后还剩0.2g钍 |
| A. | 火星探测器的质量 | B. | 引力常量 | ||
| C. | 火星探测器与火星间的万有引力 | D. | 火星的第一宇宙速度 |
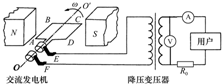 某住宅区的应急供电系统,由交流发电机和理想降压变压器组成.发电机中矩形线圈所围的面积为S,匝数为N,电阻不计.它可绕水平轴OO′在磁感应强度为B的水平匀强磁场中以角速度ω匀速转动.矩形线圈通过滑环连接变压器.R0表示输电线的电阻,其它部分电阻忽略不计.以线圈平面与磁场平行时为计时起点,下列判断正确的是( )
某住宅区的应急供电系统,由交流发电机和理想降压变压器组成.发电机中矩形线圈所围的面积为S,匝数为N,电阻不计.它可绕水平轴OO′在磁感应强度为B的水平匀强磁场中以角速度ω匀速转动.矩形线圈通过滑环连接变压器.R0表示输电线的电阻,其它部分电阻忽略不计.以线圈平面与磁场平行时为计时起点,下列判断正确的是( )| A. | 若发电机线圈某时刻处于图示位置,变压器原线圈的电流瞬时值最小 | |
| B. | 经过半个周期,电压表读数为0 | |
| C. | 发电机线圈感应电动势的瞬时值表达式为e=NBSωsinωt | |
| D. | 当用户数目增多时,电压表的读数不变,电流表读数变大 |
 某同学在“探究功与物体速度变化的关系”实验中,设计了如图甲所示的实验,将纸带固定在重物上,让纸带穿过电火花计时器或打点计时器,先用手提着纸带,使重物静止在靠近计时器的地方,然后接通电源,松开纸带,让重物自由下落,计时器就在纸带上打下一系列小点,得到的纸带如图乙所示,O为计时器打下的第1个点,该同学对数据进行了下列处理:取OA=AB=BC,并根据纸带算出了A、B、C三点的速度分别为vA=0.12m/s,vB=0.17m/s,vC=0.21m/s,根据以上数据,你能否大致判断W∝v2?
某同学在“探究功与物体速度变化的关系”实验中,设计了如图甲所示的实验,将纸带固定在重物上,让纸带穿过电火花计时器或打点计时器,先用手提着纸带,使重物静止在靠近计时器的地方,然后接通电源,松开纸带,让重物自由下落,计时器就在纸带上打下一系列小点,得到的纸带如图乙所示,O为计时器打下的第1个点,该同学对数据进行了下列处理:取OA=AB=BC,并根据纸带算出了A、B、C三点的速度分别为vA=0.12m/s,vB=0.17m/s,vC=0.21m/s,根据以上数据,你能否大致判断W∝v2?