题目内容
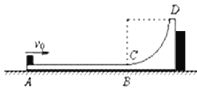
【题目】如图所示是某次四驱车比赛的一段轨道.四驱车(可视为质点)的质量m=1.0kg,额定功率为P=7W.四驱车从水平平台上A点以额定功率启动,经过一段时间t1=1.5s后关闭发动机,四驱车由平台边缘B点飞出后,恰能沿竖直光滑圆弧轨道CDE上C点的切线方向飞入圆形轨道.已知四驱车在AB段运动时的阻力f恒为1N,AB间的距离L=6m,圆轨道的半径R=1m,∠COD=53°,重力加速度g取10m/s2,不计空气阻力.sin53°=0.8,cos53°=0.6,求:
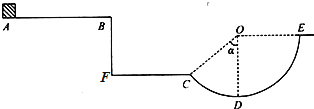
(1)四驱车从B点飞出时的速度VB的大小;
(2)四驱车从B点运动到C点的时间t2;
(3)四驱车第一次经过D点时对轨道的压力大小.
【答案】(1)vB=3m/s (2) t2=0.4s (3)压力为43N
【解析】
(1)小车离开B点做平抛运动,根据平行四边形定则求出水平分速度,从而得出B点的速度;
(2)从B点运动到C点,做的是平抛运动,根据平抛运动的规律计算时间的大小;
(3)根据机械能守恒定律求出D点的速度,通过牛顿第二定律求出支持力的大小,从而得出压力的大小.
(1)从A到B根据动能定理有![]() 代入数据得:vB=3m/s
代入数据得:vB=3m/s
(2)B到C做平抛运动,C点时沿竖直方向的分速度为:vy=vBtan53°=4m/s
vy=gt
代入数据得:t=0.4s
(3)滑块到C点时的速度为:vC=![]() =5m/s
=5m/s
从C到D过程中机械能守恒,有:![]()
又![]()
可得:F=43N
由牛顿第三定律可知,四驱车第一次经过D点时对轨道的压力大小为43N
故本题答案是:(1)vB=3m/s (2) t2=0.4s (3)压力为43N

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目