Question

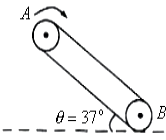
【题目】一个内壁光滑的圆锥形筒的轴线垂直水平面，圆锥筒固定，有质量相同的小球A和B沿着筒的内壁在水平面内做匀速圆周运动，如图所示，A的运动半径较大，则（ ）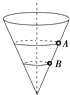

A.A球的角速度必小于B球的角速度
B.A球的线速度必小于B球的线速度
C.A球的运动周期必大于B球的运动周期
D.A球对筒壁的压力必大于B球对筒壁的压力

Answer 1

【答案】A,C
【解析】解：A、以小球为研究对象，对小球受力分析，小球受力如图所示，

由牛顿第二定律得：mgtanθ=m ，

解得：v= ，

则ω= = ，

T= =2π ，

由图示可知，对于AB两个球来说，重力加速度g与角θ相同，

A的转动半径大，B的半径小，因此，A的角速度小于B的角速度，A的线速度大于B的线速度，A的周期大于B的周期，AC符合题意，B，不符合题意；

D、由受力分析图可知，球受到的支持力FN= ，由于两球的质量m与角度θ相同，则桶壁对AB两球的支持力相等，由牛顿第三定律可知，两球对桶壁的压力相等，D不符合题意；

故答案为：AC．

做匀速圆周运动的物体，合外力等于向心力。根据向心力的公式，以及小球的受力情况，两个小球的向心力大小相等。周期越长的，半径越小。