题目内容
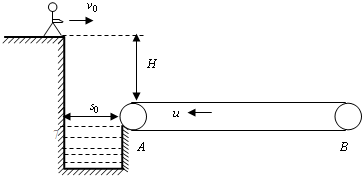
某电视台娱乐节目,选手要从较高的平台上以水平速度跃出后,落在水平传送带上,已知平台与传送带高度差H=1.8m,水池宽度S0=1.05m,传送带AB间的距离L0=21m,由于传送带足够粗糙,假设人落到传送带上后瞬间相对传送带静止,经过一个△t=0.5s反应时间后,立刻以a=2m/s2恒定向右加速度跑至传送带最右端.
(1)若传送带静止,选手以v0=3m/s水平速度从平台跃出,求从开始跃出到跑至传送带右端经历的时间.
(2)若传送带以u=1m/s的恒定速度向左运动,选手不从传送带左侧掉下落水,他从高台上跃出的水平速度v1至少多大?
(1)若传送带静止,选手以v0=3m/s水平速度从平台跃出,求从开始跃出到跑至传送带右端经历的时间.
(2)若传送带以u=1m/s的恒定速度向左运动,选手不从传送带左侧掉下落水,他从高台上跃出的水平速度v1至少多大?

分析:(1)根据平抛运动的规律求出平抛运动的时间以及水平位移,从而得出匀加速直线运动的位移,结合位移时间公式求出匀加速运动的时间,结合平抛运动的时间和反应时间求出从开始跃出到跑至传送带右端经历的时间.
(2)根据反应时间内的位移以及匀减速运动到零的位移得出平抛运动的最小位移,结合平抛运动的规律求出平抛运动的最小速度.
(2)根据反应时间内的位移以及匀减速运动到零的位移得出平抛运动的最小位移,结合平抛运动的规律求出平抛运动的最小速度.
解答:解:(1)根据H=
gt12 得t1=0.6s,
平抛运动的水平位移s1=v0t1=3×0.6m=1.8m,
匀加速直线运动的过程有:s2=L0-(s1-s0)=
at22
得:t2=4.5s.
则总时间t=t1+t2+△t=5.6s.
(2)选手落至传送带在0.5s反应时间内向左的位移大小 s1′=μ△t=0.5m
然后向左减速至速度为零,向左发生的位移为s2′,
则s2′=
=0.25m,
选手不从传送带左侧掉下,平抛水平位移 s≥s0+s1′+s2′=1.8m,
则v1=
≥3m/s.
答:(1)从开始跃出到跑至传送带右端经历的时间为5.6s.
(2)他从高台上跃出的水平速度v1至少为3m/s.
| 1 |
| 2 |
平抛运动的水平位移s1=v0t1=3×0.6m=1.8m,
匀加速直线运动的过程有:s2=L0-(s1-s0)=
| 1 |
| 2 |
得:t2=4.5s.
则总时间t=t1+t2+△t=5.6s.
(2)选手落至传送带在0.5s反应时间内向左的位移大小 s1′=μ△t=0.5m
然后向左减速至速度为零,向左发生的位移为s2′,
则s2′=
| u2 |
| 2a |
选手不从传送带左侧掉下,平抛水平位移 s≥s0+s1′+s2′=1.8m,
则v1=
| s |
| t1 |
答:(1)从开始跃出到跑至传送带右端经历的时间为5.6s.
(2)他从高台上跃出的水平速度v1至少为3m/s.
点评:解决本题的关键分析出选手的运动情况,知道平抛运动在水平方向和竖直方向上的运动规律,然后根据平抛运动和运动学公式求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2011?洪山区模拟)如图所示,参加某电视台娱乐节目的选手从较高的平台上以水平速度跃出后,落在水平传送带上.已知平台与传送带的高度差H=1.8m,水池宽度s0=1.2m,传送带AB间的距离L0=20m.由于传送带足够粗糙,假设选手落到传送带上后瞬间相对传送带静止,经过△t=1.0s反应时间后,立刻以a=2m/s2恒定向右的加速度跑至传送带最右端.
(2011?洪山区模拟)如图所示,参加某电视台娱乐节目的选手从较高的平台上以水平速度跃出后,落在水平传送带上.已知平台与传送带的高度差H=1.8m,水池宽度s0=1.2m,传送带AB间的距离L0=20m.由于传送带足够粗糙,假设选手落到传送带上后瞬间相对传送带静止,经过△t=1.0s反应时间后,立刻以a=2m/s2恒定向右的加速度跑至传送带最右端.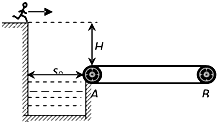 如图所示,参加某电视台娱乐节目的选手从较高的平台上以水平速度跃出后,落在水平传送带上.已知平台与传送带的高度差H=1.8m,水池宽度s0=1.2m,传送带AB间的距离L0=20m.由于传送带足够粗糙,假设选手落到传送带上后瞬间相对传送带静止,经过△t=1.0s反应时间后,立刻以a=2m/s2恒定向右的加速度跑至传送带最右端.
如图所示,参加某电视台娱乐节目的选手从较高的平台上以水平速度跃出后,落在水平传送带上.已知平台与传送带的高度差H=1.8m,水池宽度s0=1.2m,传送带AB间的距离L0=20m.由于传送带足够粗糙,假设选手落到传送带上后瞬间相对传送带静止,经过△t=1.0s反应时间后,立刻以a=2m/s2恒定向右的加速度跑至传送带最右端.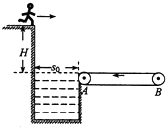 如图所示,参加某电视台娱乐节目的选手从较高的平台上以水平速度跃出后,落在水平传送带上.已知平台与传送带的高度差H=1.8m,水池宽度s0=1.2m,传送带AB间的距离L0=16.6m.由于传送带足够粗糙,选手落到传送带上后瞬间相对传送带静止,经过△t=1.0s反应时间后,立即以水平向右的加速度a=2m/s2跑至传送带最右端.若传送带以v=2m/s的恒定速度向左运动,若要选手不致落入水池,求选手从高台上跃出的最小水平速度.(计算结果保留2位有效数字)
如图所示,参加某电视台娱乐节目的选手从较高的平台上以水平速度跃出后,落在水平传送带上.已知平台与传送带的高度差H=1.8m,水池宽度s0=1.2m,传送带AB间的距离L0=16.6m.由于传送带足够粗糙,选手落到传送带上后瞬间相对传送带静止,经过△t=1.0s反应时间后,立即以水平向右的加速度a=2m/s2跑至传送带最右端.若传送带以v=2m/s的恒定速度向左运动,若要选手不致落入水池,求选手从高台上跃出的最小水平速度.(计算结果保留2位有效数字)