题目内容
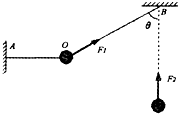 如图所示,水平细线OA和倾斜细线OB将小球悬挂于0点,小球处于平衡状态.细线OB与竖直方向的夹角θ=60°,对小球的拉力为F1.烧断水平细线,当小球摆到最低点时,细线OB对小球的拉力为F2.不计细线的伸长及一切阻力,则F1与F2的大小之比等于
如图所示,水平细线OA和倾斜细线OB将小球悬挂于0点,小球处于平衡状态.细线OB与竖直方向的夹角θ=60°,对小球的拉力为F1.烧断水平细线,当小球摆到最低点时,细线OB对小球的拉力为F2.不计细线的伸长及一切阻力,则F1与F2的大小之比等于
- A.1:1
- B.1:2
- C.2:3
- D.1:3
A
分析:烧断水平细线前,小球处于平衡状态,合力为零,根据平衡条件求F1.烧断水平细线,当小球摆到最低点时,由机械能守恒定律求出速度,再由牛顿牛顿第二定律求F2.
解答:烧断水平细线前,小球处于平衡状态,合力为零,根据平衡条件得:F1cosθ=mg,得F1=2mg;
烧断水平细线,设小球摆到最低点时速度为v,绳长为L.小球摆到最低点的过程中,由机械能守恒定律得:
mgL(1-cosθ)=
在最低点,有 F2-mg=m
联立解得 F2=2mg;
故选A
点评:本题是共点力平衡和机械能守恒、牛顿第二定律的综合,要善于分析物体的状态和运动过程,准确选择解题规律.
分析:烧断水平细线前,小球处于平衡状态,合力为零,根据平衡条件求F1.烧断水平细线,当小球摆到最低点时,由机械能守恒定律求出速度,再由牛顿牛顿第二定律求F2.
解答:烧断水平细线前,小球处于平衡状态,合力为零,根据平衡条件得:F1cosθ=mg,得F1=2mg;
烧断水平细线,设小球摆到最低点时速度为v,绳长为L.小球摆到最低点的过程中,由机械能守恒定律得:
mgL(1-cosθ)=

在最低点,有 F2-mg=m

联立解得 F2=2mg;
故选A
点评:本题是共点力平衡和机械能守恒、牛顿第二定律的综合,要善于分析物体的状态和运动过程,准确选择解题规律.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
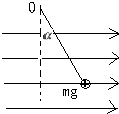 如图所示,绝缘细线一端固定于O点,另一端连接一带电荷量为q,质量为m的带正电小球,该装置处于水平向右的匀强电场中,小球静止时细线与竖直方向成α角,求细线的拉力F及匀强电场的电场强度E.
如图所示,绝缘细线一端固定于O点,另一端连接一带电荷量为q,质量为m的带正电小球,该装置处于水平向右的匀强电场中,小球静止时细线与竖直方向成α角,求细线的拉力F及匀强电场的电场强度E.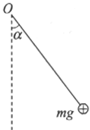 如图所示,绝缘细线一端固定于O点,另一端连接一带电荷量为q,质量为m的带正电小球,空间存在一水平方向的匀强电场,要使带电小球静止时细线与竖直方向成а角(如图),则匀强电场的方向如何?大小是多少?
如图所示,绝缘细线一端固定于O点,另一端连接一带电荷量为q,质量为m的带正电小球,空间存在一水平方向的匀强电场,要使带电小球静止时细线与竖直方向成а角(如图),则匀强电场的方向如何?大小是多少?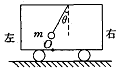 A.P与O重合
A.P与O重合 如图所示,一细线上端固定,下端拴一个带负电的小球,使小球在水平面内作圆周运动,运动方向为俯视逆时针方向,则悬点O处的磁场方向是[ ]
如图所示,一细线上端固定,下端拴一个带负电的小球,使小球在水平面内作圆周运动,运动方向为俯视逆时针方向,则悬点O处的磁场方向是[ ]