题目内容
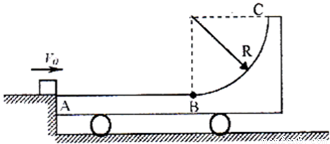
如图所示,一平板小车静止在光滑的水平地面上,车上固定着半径为R=0.7m的四分之一竖直光滑圆弧轨道,小车与圆弧轨道的总质量M为2kg,小车上表面的AB部分是长为1.0m的粗糙水平面,圆弧与小车上表面在B处相切.现有质量m=1kg的滑块(视为质点)以 v=3m/s的水平初速度从与车的上表面等高的固定光滑平台滑上小车,滑块恰好在B处相对小车静止,g=10m/s2.(1)求滑块与小车之间的动摩擦因数μ和此过程小车在水平面上滑行的距离s;
(2)要使滑块滑上小车后不从C处飞出,求初速度v应满足的条件.
【答案】分析:(1)当v=3m/s时,滑块在B处相对小车静止时的共同速度为v1,由动量守恒定律列出等式,分别对滑块和小车运用动能定理求解
(2)要使滑块刚好不从圆弧轨道上端C点飞出,滑块到C点时,二者具有相同的速度,由系统水平方向的动量守恒和系统能量守恒列出等式求解.
解答:解:(1)当v=3m/s时,滑块在B处相对小车静止时的共同速度为v1,由动量守恒定律:mv=(M+m)v1…①
对滑块,由动能定理: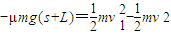 …②
…②
对小车,由动能定理: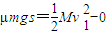 …③
…③
由①②③得: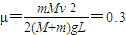 …④
…④
 m…⑤
m…⑤
(2)要使滑块刚好不从圆弧轨道上端C点飞出,滑块到C点时,二者具有相同的速度设为v2,
由系统水平方向的动量守恒:mv=(M+m)v2…⑥
由系统能量守恒: …⑦
…⑦
由④⑥⑦得: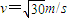
要使滑块不从圆弧轨道上端C点飞出,必须满足: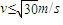
答:(1)滑块与小车之间的动摩擦因数μ是0.3,此过程小车在水平面上滑行的距离是 m;
m;
(2)要使滑块滑上小车后不从C处飞出,初速度v应满足的条件是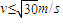 .
.
点评:解决该题关键要能够清楚物体的运动情况,运用动量守恒定律和动能定理求解.
(2)要使滑块刚好不从圆弧轨道上端C点飞出,滑块到C点时,二者具有相同的速度,由系统水平方向的动量守恒和系统能量守恒列出等式求解.
解答:解:(1)当v=3m/s时,滑块在B处相对小车静止时的共同速度为v1,由动量守恒定律:mv=(M+m)v1…①
对滑块,由动能定理:
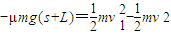 …②
…②对小车,由动能定理:
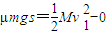 …③
…③由①②③得:
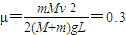 …④
…④ m…⑤
m…⑤(2)要使滑块刚好不从圆弧轨道上端C点飞出,滑块到C点时,二者具有相同的速度设为v2,
由系统水平方向的动量守恒:mv=(M+m)v2…⑥
由系统能量守恒:
 …⑦
…⑦由④⑥⑦得:
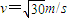
要使滑块不从圆弧轨道上端C点飞出,必须满足:
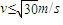
答:(1)滑块与小车之间的动摩擦因数μ是0.3,此过程小车在水平面上滑行的距离是
 m;
m;(2)要使滑块滑上小车后不从C处飞出,初速度v应满足的条件是
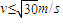 .
.点评:解决该题关键要能够清楚物体的运动情况,运用动量守恒定律和动能定理求解.

练习册系列答案
相关题目
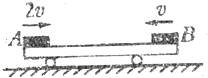 如图所示,一平板小车静止在光滑的水平面上,质量均为m的物体A、B分别以2v和v的初速度、沿同一直线同时从小车两端相向水平滑上小车.设两物体与小车间的动摩擦因数均为μ,小车质量也为m,最终物体A、B都停在小车上(若A、B相碰,碰后一定粘在一起)求:
如图所示,一平板小车静止在光滑的水平面上,质量均为m的物体A、B分别以2v和v的初速度、沿同一直线同时从小车两端相向水平滑上小车.设两物体与小车间的动摩擦因数均为μ,小车质量也为m,最终物体A、B都停在小车上(若A、B相碰,碰后一定粘在一起)求: 如图所示,一平板小车静止在光滑的水平面上,质量均为m的物体A、B分别以2v和v的初速度、沿同一直线同时从小车两端相向水平滑上小车.设两物体与小车间的动摩擦因数均为μ,小车质量也为m,最终物体A、B都停在小车上(若A、B相碰,碰后一定粘在一起).求:
如图所示,一平板小车静止在光滑的水平面上,质量均为m的物体A、B分别以2v和v的初速度、沿同一直线同时从小车两端相向水平滑上小车.设两物体与小车间的动摩擦因数均为μ,小车质量也为m,最终物体A、B都停在小车上(若A、B相碰,碰后一定粘在一起).求: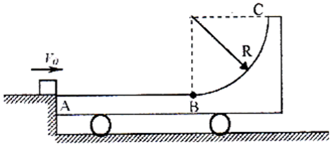
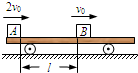 如图所示,一平板小车静止在光滑水平面上,质量均为m的物体A、B分别以2v0和v0的初速度,沿同一直线同时同向水平滑上小车,刚开始滑上小车的瞬间,A位于小车的最左边,B位于距小车左边l处.设两物体与小车间的动摩擦因数均为μ,小车的质量也为m,最终物体A、B都停在小车上.求:
如图所示,一平板小车静止在光滑水平面上,质量均为m的物体A、B分别以2v0和v0的初速度,沿同一直线同时同向水平滑上小车,刚开始滑上小车的瞬间,A位于小车的最左边,B位于距小车左边l处.设两物体与小车间的动摩擦因数均为μ,小车的质量也为m,最终物体A、B都停在小车上.求: