题目内容
3.一人登楼,其登楼的速度与登楼的高度成反比,已知每层楼的高度为3m,该人登到第三层楼(6m)时的速度为5m/s.则该人登到第八层楼(21m)时的速度为1.43m/s;他从第三层楼到第八层楼所用的时间为6.75s.(设该人在同一层楼运动的时间不计)分析 由题意可知速度和高度成反比,根据给出的高度和速度可明确比例系数则可求出8楼时的速度,再作出h-$\frac{1}{v}$图象,根据v-t图象面积的迁移应用则可求得时间大小.
解答  解:由题意可知,速度与楼高成反比;当楼高6m时速度为5m/s,则由v=$\frac{k}{h}$可知,k=5×6=30;因此当数高为21m时,速度v2=$\frac{30}{21}$=1.43m/s;
解:由题意可知,速度与楼高成反比;当楼高6m时速度为5m/s,则由v=$\frac{k}{h}$可知,k=5×6=30;因此当数高为21m时,速度v2=$\frac{30}{21}$=1.43m/s;
作出h-$\frac{1}{v}$图象如图所示,根据图象规律以及h=vt可知,图象与横坐标的面积应表示时间,则由图可知:t=$\frac{6+21}{2}×0.5$=6.75s.
故答案为;1.43;6.75.
点评 本题考查匀变速直线运动图象的应用,要注意明确v-t图象中面积表示位移,利用迁移应用规律可知h-$\frac{1}{v}$图象中面积可以表示时间.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.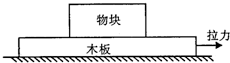 如图所示,一足够长的木板静止在光滑水平面上,一物块静止在木板上,木板和物块间有摩擦.现用水平力向右拉木板,当物块相对木板滑动了一段距离但仍有相对运动时撤掉拉力,下列关于此后木板和物块相对于水平面的运动情况的说法中正确的是( )
如图所示,一足够长的木板静止在光滑水平面上,一物块静止在木板上,木板和物块间有摩擦.现用水平力向右拉木板,当物块相对木板滑动了一段距离但仍有相对运动时撤掉拉力,下列关于此后木板和物块相对于水平面的运动情况的说法中正确的是( )
 如图所示,一足够长的木板静止在光滑水平面上,一物块静止在木板上,木板和物块间有摩擦.现用水平力向右拉木板,当物块相对木板滑动了一段距离但仍有相对运动时撤掉拉力,下列关于此后木板和物块相对于水平面的运动情况的说法中正确的是( )
如图所示,一足够长的木板静止在光滑水平面上,一物块静止在木板上,木板和物块间有摩擦.现用水平力向右拉木板,当物块相对木板滑动了一段距离但仍有相对运动时撤掉拉力,下列关于此后木板和物块相对于水平面的运动情况的说法中正确的是( )| A. | 物块线向右做匀减速直线运动,后做匀速直线运动 | |
| B. | 物块线向右做匀加速直线运动,后做匀速直线运动 | |
| C. | 木板线向右做匀减速直线运动,后做匀速直线运动 | |
| D. | 物块和木板立即以相同的速度做匀速直线运动 |
11.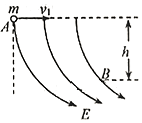 空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,若A、B两点之间的高度差为h,则以下判断中正确的是( )
空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,若A、B两点之间的高度差为h,则以下判断中正确的是( )
 空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,若A、B两点之间的高度差为h,则以下判断中正确的是( )
空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,若A、B两点之间的高度差为h,则以下判断中正确的是( )| A. | A、B两点的电场强度和电势大小关系为EA<EB、φA>φB | |
| B. | 若带正电,则电场力一定做负功 | |
| C. | A、B两点间的电势差为$\frac{m}{2q}$(v22-v12-2gh) | |
| D. | 小球从A运动到B点的过程中电场力做的功为$\frac{1}{2}$mv22-$\frac{1}{2}$mv2-mgh |
8. 搭载着航天员景海鹏、陈冬的神舟十一号载人飞船在酒泉卫星发射中心搭乘长征二号FY11火箭成功发射,在多次调整姿态后,于2016年10月19日3时31分顺利完成与天宫二号的对接任务,如图所示,已知天宫二号圆周轨道离地393公里,下列说法正确的是( )
搭载着航天员景海鹏、陈冬的神舟十一号载人飞船在酒泉卫星发射中心搭乘长征二号FY11火箭成功发射,在多次调整姿态后,于2016年10月19日3时31分顺利完成与天宫二号的对接任务,如图所示,已知天宫二号圆周轨道离地393公里,下列说法正确的是( )
 搭载着航天员景海鹏、陈冬的神舟十一号载人飞船在酒泉卫星发射中心搭乘长征二号FY11火箭成功发射,在多次调整姿态后,于2016年10月19日3时31分顺利完成与天宫二号的对接任务,如图所示,已知天宫二号圆周轨道离地393公里,下列说法正确的是( )
搭载着航天员景海鹏、陈冬的神舟十一号载人飞船在酒泉卫星发射中心搭乘长征二号FY11火箭成功发射,在多次调整姿态后,于2016年10月19日3时31分顺利完成与天宫二号的对接任务,如图所示,已知天宫二号圆周轨道离地393公里,下列说法正确的是( )| A. | 飞船发射速度可能会超过11.2km/s | |
| B. | 飞船需要在较低的轨道上向后喷出炙热气体,才能完成与天宫二号的对接 | |
| C. | 飞船与天宫二号在同一轨道时向后喷出炙热气体,才能完成与天宫二号的对接 | |
| D. | 若已知飞船与天宫二号的“组合体”运行周期T、离地高度h、地球半径R,地球质量M,可求出“组合体”的质量 |
12.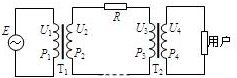 如图所示,有一台交流发电机E,通过理想升压变压器T1和理想降压变压器T2向远处用户供电,输电线的总电阻为R.T1的输入电压和输入功率分别为U1和P1,它的输出电压和输出功率分别为U2和P2;T2的输入电压和输入功率分别为U3和P3,它的输出电压和输出功率分别为U4和P4.设T1的输入电压U1一定,当用户消耗的电功率变大时,有( )
如图所示,有一台交流发电机E,通过理想升压变压器T1和理想降压变压器T2向远处用户供电,输电线的总电阻为R.T1的输入电压和输入功率分别为U1和P1,它的输出电压和输出功率分别为U2和P2;T2的输入电压和输入功率分别为U3和P3,它的输出电压和输出功率分别为U4和P4.设T1的输入电压U1一定,当用户消耗的电功率变大时,有( )
 如图所示,有一台交流发电机E,通过理想升压变压器T1和理想降压变压器T2向远处用户供电,输电线的总电阻为R.T1的输入电压和输入功率分别为U1和P1,它的输出电压和输出功率分别为U2和P2;T2的输入电压和输入功率分别为U3和P3,它的输出电压和输出功率分别为U4和P4.设T1的输入电压U1一定,当用户消耗的电功率变大时,有( )
如图所示,有一台交流发电机E,通过理想升压变压器T1和理想降压变压器T2向远处用户供电,输电线的总电阻为R.T1的输入电压和输入功率分别为U1和P1,它的输出电压和输出功率分别为U2和P2;T2的输入电压和输入功率分别为U3和P3,它的输出电压和输出功率分别为U4和P4.设T1的输入电压U1一定,当用户消耗的电功率变大时,有( )| A. | U2不变,U3变小 | B. | U2减小,U4变大 | C. | P2变大,P3变大 | D. | P1不变,P2变小 |
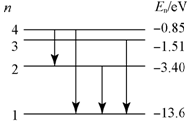 如图所示为氢原子最低的四个能级图:
如图所示为氢原子最低的四个能级图: 如图所示,一装满水的水槽放在太阳光下,将平面镜M斜放入水中,调整其倾斜角度,使一束太阳光从O点经水面折射和平面镜反射,然后经水面折射回到空气中,最后射到槽左侧上方的屏幕N上,即可观察到彩色光带.如果逐渐增大平面镜的倾角θ,各色光将陆续消失.已知所有光线均在同一竖直平面.
如图所示,一装满水的水槽放在太阳光下,将平面镜M斜放入水中,调整其倾斜角度,使一束太阳光从O点经水面折射和平面镜反射,然后经水面折射回到空气中,最后射到槽左侧上方的屏幕N上,即可观察到彩色光带.如果逐渐增大平面镜的倾角θ,各色光将陆续消失.已知所有光线均在同一竖直平面. 如图所示,某回旋加速器的两个半圆金属盒处于与盒面垂直的匀强磁场中,两金属盒间存在交变电场,用其加速质子.已知金属盒的半径R为16cm,磁场的磁感应强度B为1.3T,质子穿过金属盒间的缝隙时加速电压U为10kV,取质子的质量m为1.6×10-27 kg,电荷量q为1.6×10-19C.求
如图所示,某回旋加速器的两个半圆金属盒处于与盒面垂直的匀强磁场中,两金属盒间存在交变电场,用其加速质子.已知金属盒的半径R为16cm,磁场的磁感应强度B为1.3T,质子穿过金属盒间的缝隙时加速电压U为10kV,取质子的质量m为1.6×10-27 kg,电荷量q为1.6×10-19C.求